トポロジーへの招待 〜 1. 座標も補助線も使わない「やわらかい幾何学」
この記事は 数学とコンピュータⅡ Advent Calendar 11日目の記事です。
こんにちは、佐野です。12月といえば Advent Calendar の季節です🎄思いつきで 数学とコンピュータ Advent Calendar Ⅰ / Ⅱ を立ち上げたところ、嬉しいことに二つともすぐに満員となりました。エントリーして下さった皆さん、ありがとうございます🙇
僕は全3回でトポロジーの考え方と計算手法を、自作のプログラムを使いながら説明していこうと思います。
- 座標も補助線も使わない「やわらかい幾何学」 ← イマココ
- 切り貼りで作る色々な曲面
- ...
このシリーズを通して トポロジーは最高に自由で楽しい数学(の一つ)である ことをお伝えできたら幸いです!
「やわらかい幾何学」って何?
「コーヒーカップを、取っ手の輪っかを残すように変形するとドーナッツの形にできる。従ってコーヒーカップとドーナッツは同じ。」と主張するのがトポロジーです。
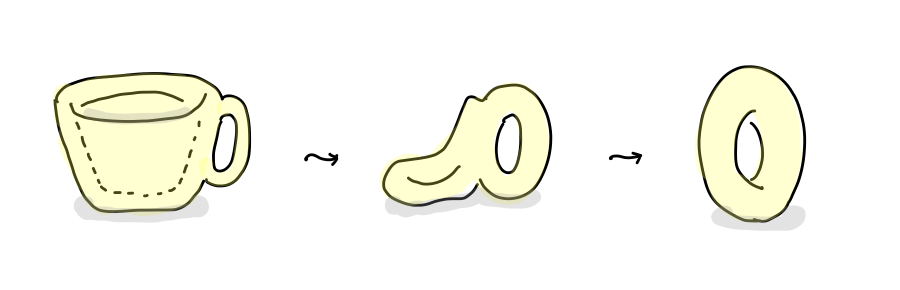
小学校や中学校で習うユークリッド幾何学では、三角形や四角形などの図形はカチッと固まっており、長さや角度を計ることはあってもグニャグニャと形を変えるようなことはしませんでした。この「硬さ」と対比して、どんな連続的な変形も受け入れるトポロジーは「やわらかい幾何学」だと言われます。
数学といえば厳密だというイメージがあると思います。しかし「コーヒーカップとドーナッツは同じ」などという主張はいかにもいい加減で、数学の土俵に乗ることすら許されないように思われます。その感覚は真っ当で、だからこそユークリッド幾何学からトポロジーの誕生まで 2,000 年以上ものときを要したのだとも言えます。トポロジーでは円や多角形などの「綺麗な図形」だけでなく、歪んだ紐や穴の空いた曲面などの「日常で目にする図形1」も数学として扱うのです。
もし数学が「綺麗な図形」しか扱わない(扱えない)お堅い学問だというイメージをお持ちなら、トポロジーの自由さ(とそれに伴う絶望的な難しさ)を前にその中世的な数学観を喜んで破砕して下さい👊
そもそも「幾何学」とは何か?
19世紀末にトポロジーを創設したアンリ・ポアンカレは 「数学とは、異なるものを同じものと見なす技術である」2と言ったそうです。…とだけ言われて「コーヒーカップとドーナッツは同じだ」と受け入れるのは難しいと思うので、少し立ち返って、私たちはどのように図形を「同じ」と見なしているのか観察してみましょう。
ユークリッド幾何学では次の二つの三角形は「同じ」であると考えます。しかし改めて考えると三角形が置かれてる位置や傾きは異なっています。どうしてこれが「同じ」だと言えるのでしょう?(難しい言葉を使わず4歳児に説明するとしたらどう言いますか?)
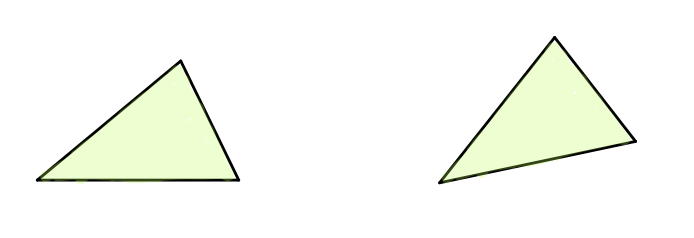
それは、左の三角形を持ち上げて動かせば右の三角形にピタッと重ねることができるからです。このとき二つの三角形は「合同」というのでした。
ユークリッド幾何学にはもう一つ「相似」という関係もあります。これは「合同」よりも広い「同じ」です。長さや面積のような「絶対的な量」でなく、長さの比や角度などの「相対的な量」を扱うときに便利な関係です。
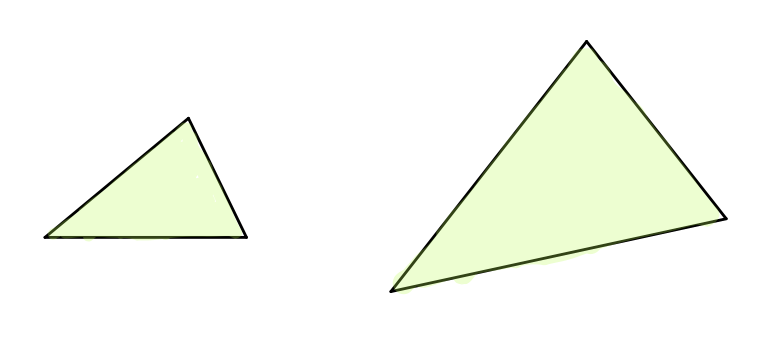
上の二つの三角形が「相似」であると言えるのは、左の三角形を縦横均等に拡大して移動することで右の三角形にピタッと重ねることができるからです。この拡大縮小が「縦横均等」であることが大切で、横方向にだけビヨーンと伸ばす3ような変形は許されていません。
この二つの例を見るだけでも、私たちは中学校までに二通りの「図形を同じと見なす技術」を学んでいることが分かります。その技術とは「特定の操作で図形を動かして一方を他方にピタッと重ねること」です。
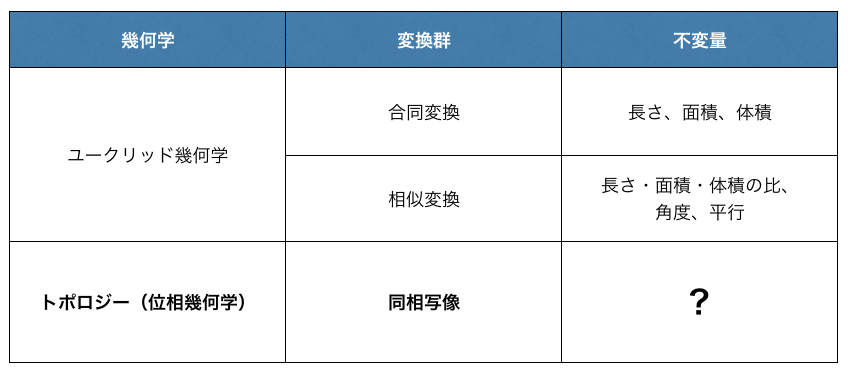
ここで19世紀の数学者クラインによる「幾何学とは何か?4」に対する答えを見てみましょう:
幾何学的性質とは、それに作用する 変換群の作用で不変に保たれる性質 のことである。
「変換群」という難しい言葉が出てきましたが、合同の例では「合同変換(回転・平行移動・鏡映)の全体」、相似の例では「相似変換(合同変換+拡大縮小)の全体」のことです。合同変換で不変に保たれるのは「長さ・面積・体積・角度」などで、相似変換で保たれるのは「長さや面積の比・角度」などです。クラインの立場では、
「ユークリッド幾何学は、合同変換や相似変換によって不変に保たれる性質を調べる学問である」
ということになります。
ではトポロジーは?
「トポロジーとは何か?」に答えるには、トポロジーにおける「同じと見なすための変換」が何かを答えれば良いことになります。それがコーヒーカップをドーナッツに変えるときに行った「連続的な変形5 6」です。ここで図形を一点に潰してしまうような変形まで認めると「全ての図形は一点と同じ」という役立たずな理論が出来上がってしまうので「可逆 = 元に戻せる」ものに限ることにします。
「可逆で、行きも戻りも連続であるような変換」
このような変換(写像)を同相写像と言い、同相写像によって移り合う二つの図形は同相(位相同型)であると言います。すると、
「トポロジーは、同相な図形同士で不変に保たれる性質(位相不変量)を調べる学問である」7
と述べることができるようになりました。つまり「コーヒーカップとドーナッツにおいて共通しているものは何か?」を問うのがトポロジーということです!
ところで「同相な図形は同じ」と見なしたいケースとはなんでしょう?その答えはトポロジーの起源とも言われる「ケーニスベルクの問題」で見ることができます。

「この7つの橋を全て、同じ橋を2度通ることなく渡り、元の所に帰ってくることができるか」という問題です。18世紀の数学者オイラーは、川で囲われた領域を点、橋で繋がっている点同士を辺とするグラフを対応させることで、それは不可能であると証明しました。
問題は「このグラフは一筆書きできるか」となり、その本質はグラフの構造、つまりどの点と点がどの繋がっているかです。実際の町における移動距離や、絵に描いたグラフの辺の長さなどは関係ありません。このケースでは「同相なグラフは同じと見なす」のが正しいアプローチだと分かります。
同相写像で保たれる性質とは?
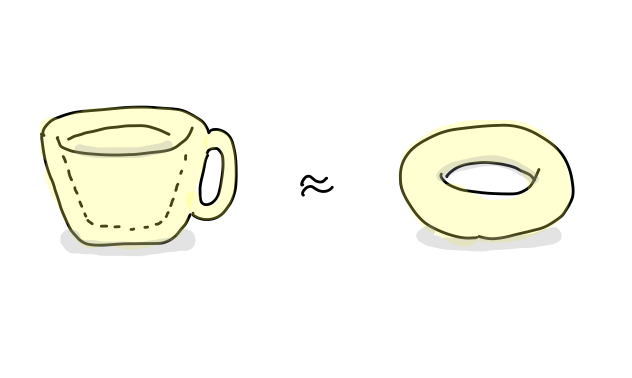
さて、二つの図形を眺めながら、何が共通していると言えるか考えてみましょう。もしこれらが粘土でできており、一方を他方に変形したのなら二つの「体積」は等しいでしょう。しかし一般に同相写像は相似変換も含んでおり、相似変換は自由に大きさを変えてしまうので「体積」は位相不変とは言えません。長さや角度を計ろうとするのも無意味です。もっと素朴に(幼児のように)考えてみましょう。
(1) 連結性
コーヒーカップもドーナッツも「一個のもの」です。コーヒーカップの取っ手の部分を切り離してしまえば図形は二つの部分に分かれます。「切り離す」というのは図形の繋がりを壊す操作ですから連続ではありません。コーヒーカップをドーナッツに変形する過程では「図形が二つ以上のものに分かれる」ことはないので「繋がった状態 = 連結性8」は保たれています。これは一つの位相不変な性質です。
(2) コンパクト性
二つの図形は有限な大きさを持つ閉じた図形です(宇宙のように無限に広がっていません)。このような図形はコンパクトであると言い、コンパクトな図形が連続写像によって無限に広がってしまうことはないので9、これも位相不変な性質です。
(3) 穴の数
ドーナッツには穴があります10。コーヒーカップも、取っ手の部分が輪っかになっているので11穴が空いています。図形を連続的に変形する過程では新たに穴が空いてしまったり埋まってしまったりすることはないので、同相写像によっては「穴の数」は保たれます。「穴の数」は上の二つと違って、数として得られる位相不変量です。
これらの性質や量は対象の図形が簡単であれば見てすぐに分かりますが、もっと複雑な図形の場合はそうは行きません。例えば 4 次元の図形が与えられて、穴が何個空いてるかを見て調べるのは一般人には不可能でしょう。何かしらもっと体系的に位相不変量を取り出す方法が欲しくなります。その本格的な手段は次回説明することにし、今回は導入として、トポロジーが創設される以前から知られていた位相不変量であるオイラー数を紹介します。
オイラー数
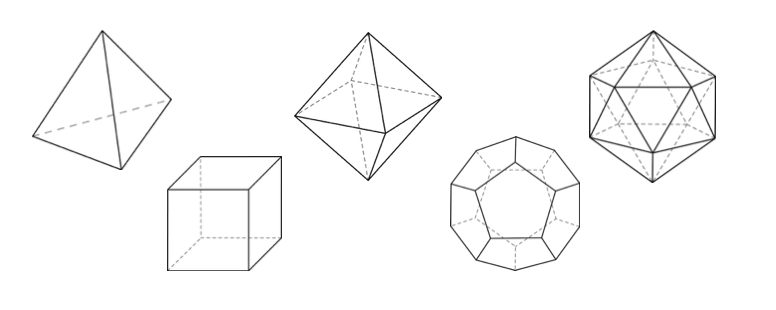
5つの正多面体があります。下の表にぞれぞれの頂点 (V: Vertex)・辺 (E: Edge)・面 (F: Face) の数が書かれています。多面体ごとにこれらの数は異なります。しかし、これらの数の組に対してある計算をすると、不思議と共通の値が出てきます。
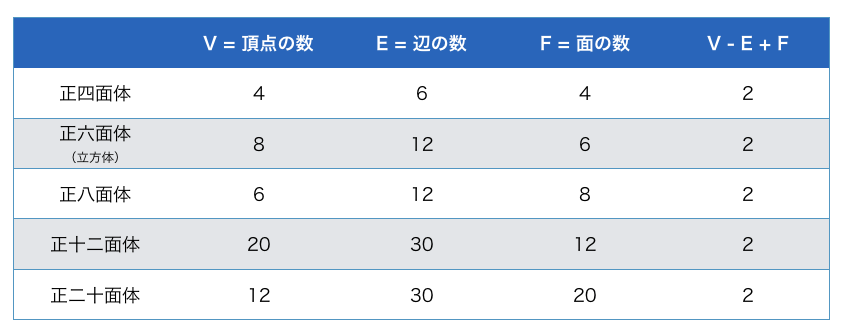
V - E + F を計算すると、全て 2 です。
どんな多面体についても V - E + F = 2 となるのでしょうか? 答えは NO です。次の図形について計算してみると、
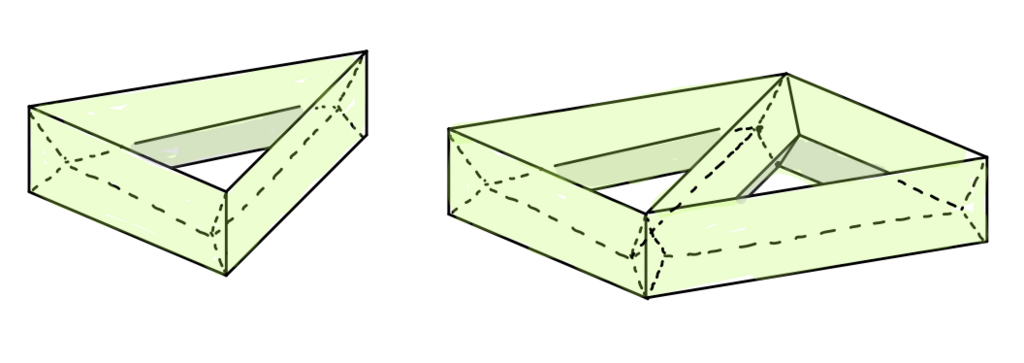
左は V - E + F = 0、右は V - E + F = -2 です。
パターン見えて来ましたね…!どうやら球面に同相な多面体は V - E + F = 2 となり(内側をプクッと膨らませるとどれも球面になりますよね)、穴の数が増えるごとに値が 2 ずつ減っていくようです。つまり穴の数を として、
となっているようです。
この量が (多面体の) オイラー数です。こんな単純な式で計算される量が位相不変であるというのは実に不思議です。例えば球面を 4 個の頂点で分割しても 5000兆個 の頂点で分割しても、オイラー数は等しく 2 となるのです。「同相であれば値が等しい」のが位相不変量なので、対偶を取れば「位相不変量が異なれば同相でない」となります。球面とトーラス(ドーナッツの表面)が同相でないという事実は、2 ≠ 0 から直ちに分かってしまう訳です。
では逆に「オイラー数が等しい図形は同相だ」と言えるでしょうか? 答えは NO です。例えばこの変な図形:

オイラー数は 0 です(数えて見てください)。どう見ても上に出てきたもの同相ではありません。 以上をまとめると、
- オイラー数は図形に対して組み合わせ的に定まる量であり、
- 同相な図形に対してはオイラー数は一致するが、
- オイラー数が一致するからといって同相とは限らない。
となります。ここで当然の疑問として、
- V - E + F という数は一体どこから出て来たのか?
- なぜこの量は位相不変となるのか?
が残ると思います。 次回、単体複体のホモロジー群 を導入し、この数の由来を探って行くことにしましょう。
完全な不変量を求めて
「オイラー数が等しくても同相とは限らない」は、ユークリッド幾何学において「合同な三角形の面積は等しい」は成り立つが「面積の等しい三角形は合同」とは限らないという事情と同じです。
しかし「三角形の合同条件」には「三辺相等」「ニ辺夾角相等」「ニ角夾辺相等」がありました。これは三角形の「辺の長さ」や「角度」などの不変量をうまく組み合わせることで 逆 が言えてしまうという強い定理です。
二つの図形の間で変換が作れるかどうかという問題は、いわば無限次元空間の中で「点」を探すことであり、一般にはとても難しいものです。一方で具体的に計算できる不変量を組み合わせることで「同型でない」だけでなく「同型である」までも判定できるとしたら、それは対象の図形がその不変量によって完全に決定されるということです。
オイラー数は位相不変量としては完全ではありませんでした。しかし対象とする図形を制限し、他の不変量と組み合わせることで、特定の図形が完全に分類できるということも次回説明します。お楽しみに!
参考図書
数学専攻でない人がトポロジーに入門するにはこちらがオススメです。特別な前提知識なく読めると思います(恐らく高校生でも)。

- 作者: 瀬山士郎
- 出版社/メーカー: 日本評論社
- 発売日: 2003/11/01
- メディア: 単行本
- 購入: 4人 クリック: 150回
- この商品を含むブログ (9件) を見る
こちらはもう少し進んだ内容で、行列を使った具体的な計算やホモロジー群の位相不変性なども扱っています。

- 作者: 田中利史・村上斉
- 出版社/メーカー: サイエンス社
- 発売日: 2005/09/25
- メディア: 雑誌
- この商品を含むブログを見る
こちらは古典的なトポロジー(単体的複体のホモロジー群・基本群)の入門書です。

- 作者: 田村一郎
- 出版社/メーカー: 岩波書店
- 発売日: 2015/08/11
- メディア: オンデマンド (ペーパーバック)
- この商品を含むブログを見る
さらに進んで学びたい人は、オンラインで入手できる A.Hatcher の "Algebraic Topology" を見てみると良いと思います。
-
もちろんトポロジーでは「日常で目にする図形」だけでなく「人間には見ることのできない図形」も扱います。↩
-
“la mathématique est l'art de donner le même nom à des choses différentes.” Science et Méthode, 1908. ↩
-
そのような変形は「アフィン変換(線形変換+平行移動)」と呼ばれ、アフィン変換で移り合う図形を同一視する幾何学が「アフィン幾何学」です。↩
-
このような「問い」が19世紀になってようやく起きた背景には、ギリシャ時代以来「ユークリッド幾何学」が唯一絶対の幾何学だと信じられてきたのに対し、18世紀以降その公理を満たさない「非ユークリッド幾何学」も成り立つことが明らかになってきたことがあります。↩
-
ユークリッド空間における「写像の連続性」を定めるのが
論法です(過去記事)。トポロジーにおいてはより一般の「位相空間(topological space)」を扱いますが、「位相」「連続写像」の厳密な定義は大幅に直観を離れてしまうので、wikipedia へのリンクだけ貼ってここでは述べないことにします。↩
-
正確には二つの図形が「同相」であることと「アイソトピック」であること(ある空間の中で同相を保ちながら一方を他方に変形できること)は異なります。「コーヒーカップとドーナッツ」の例では
の中でアイソトピーを作っており、その結果として二つの図形は同相となっています。↩
-
トポロジーでは「同相」よりも遥かに広い「ホモトピー同値」という同値関係も扱います。例えば
と 1点、円周とメビウスの帯などは互いにホモトピー同値になります。↩
-
「有界 = 有限の大きさを持っている」だけではダメです。例えば
内の半径 1 の円板で境界の円周を除いたもの(開円板)は
と同相になります。あるいは長さ 1 の開区間
は実数直線
と同相です。面積や長さは等しくても、境界を含んでいるか否か(図形が閉じているか否か)で位相的な性質は決定的に変わってしまいます。↩
-
Oxford Dictionary における doughnut の定義 には “Typically in the shape of a ball or ring.” とあるので、「穴が空いてる」ことがその定義に含まれる訳ではないようです。↩