トポロジーへの招待 〜 3. ホモロジー群の構成とオイラー数の正体
最近では、トポロジーの天使と抽象代数学の悪魔との葛藤が、すべての数学の研究で起きている。1
20世紀の数学者ヘルマン・ワイルの言葉です。過去2回の記事を読んでくれた方は「トポロジー楽しそう!」と感じてくれたことと思います。これまでは「トポロジーの天使」の紹介でした。
今回は「抽象代数学の悪魔」の話です。
…と言っても「悪魔の力」のほんの一部を紹介する程度です。図形の位相不変量が具体的に計算できる面白さをお見せしたい。天使と悪魔の二面性こそがトポロジーの(あるいは数学の)の面白さだと思うので、それが共有できたら幸いです😙
この記事は 数学とコンピュータ Advent Calendar 25日目の記事です。
前回の復習
前回は球面・トーラスなどのお馴染みの曲面から、射影平面・クラインの壷など日常では見ることのできない曲面まで色々と紹介し、これらの閉曲面がオイラー数と向きづけ可能性だけで分類できることを述べました。
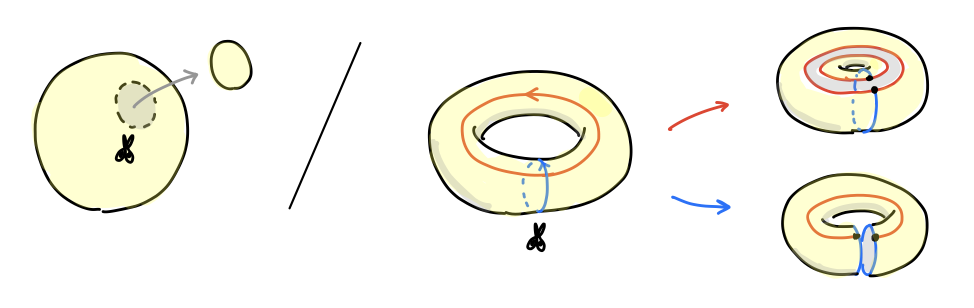
閉曲面を分類するための指針として「キリトリ線に沿って曲面を切って、曲面が二つに分かれないものはどれだけあるか?」を考察しました。今回はこれらの位相不変量をアルゴリズミックに取り出す方法として(単体複体の)ホモロジー群 を導入します。
線形代数(ベクトルと行列)の基本的な知識を前提としますが、適宜補足を入れてあるのでついてきて下さい👍
チェイン複体の構成
1次チェイン
「曲面の一部分の境界でないキリトリ線」 がどれだけあるかを調べたい。曲面上の曲線の取り方は無限にあるので、このままだと掴み所がありません。そこで曲面を CG のポリゴンメッシュのように三角形で分割して、その辺に沿った曲線を考えることにします。こうすれば考えうる曲線は有限個になるので、組み合わせ的に問題が解決できそうです。
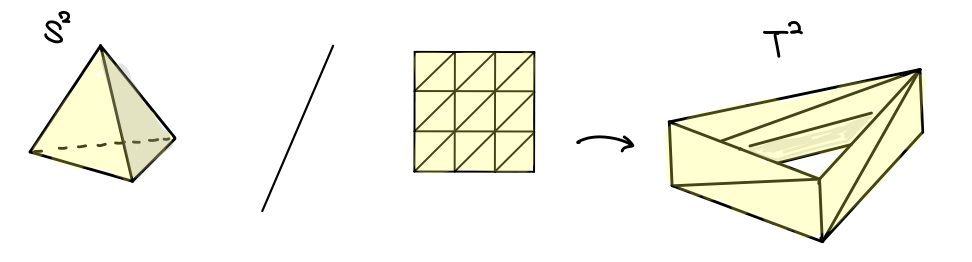
球面は四面体の境界とし、トーラスは図のように 18個 の三角形で分割します2。
これらの辺上の曲線を表示するために、各辺に名前をつけて向きを定め、曲線を足し算の形で現します(逆向きに進む場合は -1 とする)。

このように足し算の形で表した辺の組を 1次チェイン と呼ぶことにします(1次は曲線の次元)。
1次サイクル
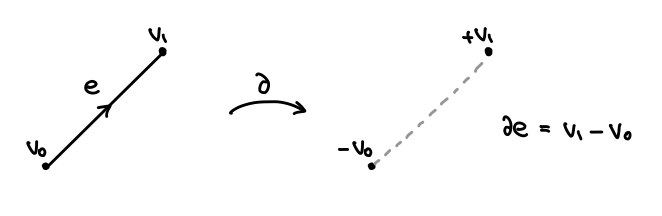
考えたい曲面上のキリトリ線は、グルッと一周して元に戻ってくる閉曲線です。各辺 に対して、始点を -1、終点を +1 で表すことにし、辺の 境界 を、
のように書くことにします。
チェイン c を表す曲線が閉じているためには、すべての始点と終点がペアになるような辺の組があればいいので、
が求める条件です。このように1次チェインであって境界が消えているものを 1次サイクル と呼びます。
2次チェインと1次バウンダリ
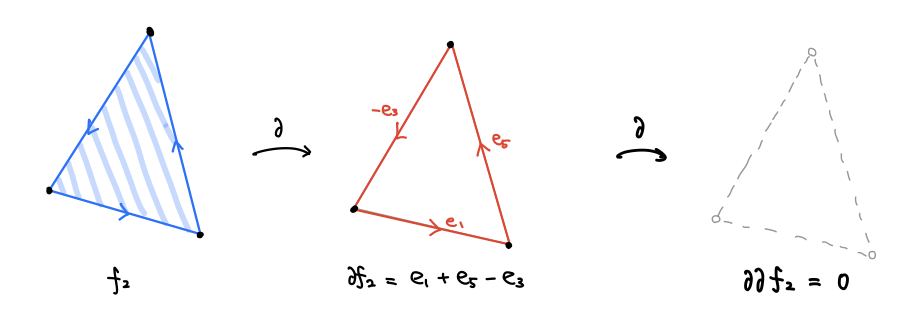
次に「曲面の一部分」を組み合わせ的に表示します。曲面を構成する三角形のすべての面にグルッと一周する向きを定めておきます。
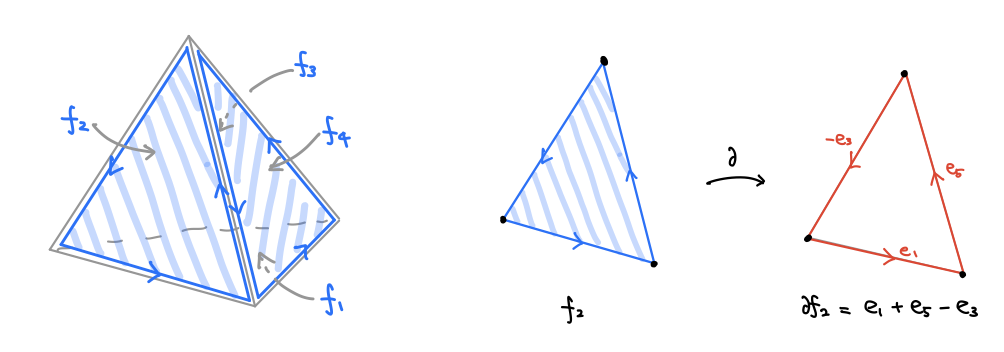
辺の境界として両端の点が出てきたように、今度は面の境界として辺が出てきます。 のように、二つの面が一つの辺を共有していて辺の向きが逆になっている場合、合わせて一つの曲面だと考えることができます。こうして三角形の面たちを足し算で閉曲面の一部(あるいは閉曲面そのもの)表したものを 2次チェイン と呼びます。
2次チェインの境界として現れる 1次チェインを、1次バウンダリと呼びます。「曲面の一部分の境界でないキリトリ線」は「1次サイクルであって、1次バウンダリでないもの」と言い換えられるようになりました。
ここで重要な事実として「1次バウンダリは、1次サイクルである」ということがあります。2次チェインの境界として現れる1次チェインは、もう一度境界を取ると消えてしまうのです。
チェイン・サイクル・バウンダリの包含関係は:
{バウンダリ} ⊂ {サイクル} ⊂ {チェイン}
となっています。私たちの問題は「1次バウンダリと1次サイクルの差がどれだけあるかを調べたい」ということだと分かりました。球面とトーラスの場合だと、
- 球面上の1次サイクルは、2次チェインの境界として現れるものしかない
- トーラス上の1次サイクルには、2次チェインの境界でないものがある
となっているのでした。
線形代数で定式化
チェインだのサイクルだの出てきてゴチャゴチャしたと思うので、上記の話を全て線形代数で定式化し直しましょう。まず曲面に三角形分割に対し、その点・辺・面に全て向きを定め、それらを基底とするベクトル空間3を考えます。これを下から順に 0次・1次・2次 チェイン群 と呼びます。

先ほど足し算で表示した 1次 サイクルは、基底に関して成分表示することで辺の個数分の次元を持つベクトルとして表示することができます:
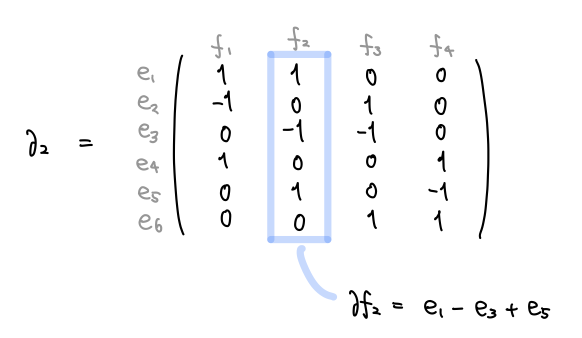
面に対してその境界の辺を取る操作を考えましたが、これは の基底である面の境界が 1 次チェイン群のどの要素に対応するかを見ることで、
から
への線形写像を定めます。これを 2次 境界写像 と言います。
線形写像は始域と終域のベクトル空間の基底によって行列表示することができます。球面の場合の1次境界写像を行列表示は次のようになります。行列を見れば、例えば の境界は
であることがわかります。
同様に、辺に対して境界の点を対応させる操作で から
への線形写像が定まります。
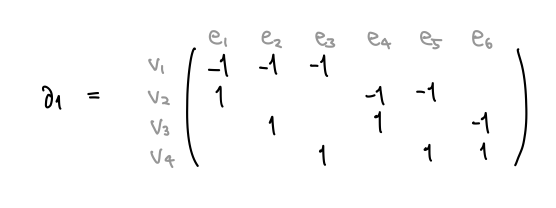
こうして曲面の三角形分割から、点・辺・面の個数だけの次元を持った 3 つのベクトル空間 チェイン群 と、その間で次数を落とす線形写像である 1次・2次 境界写像 を定義することができました。
サイクル(核)とバウンダリ(像)
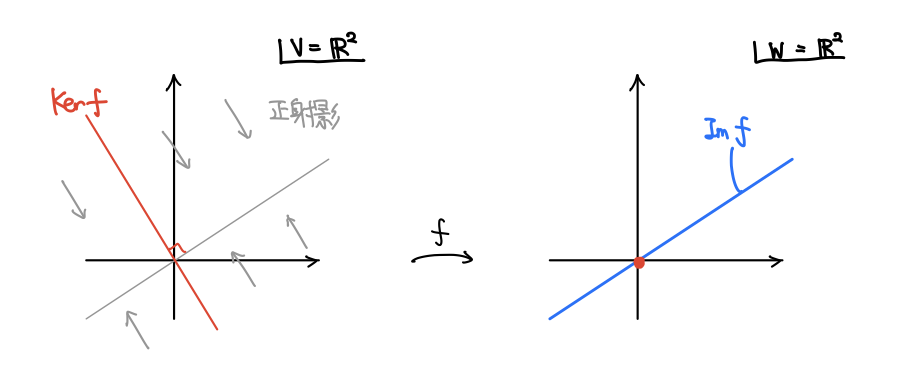
(線形代数の一般論)線形写像 に対して、
によって
に移ってしまう
の要素全体を
の 核 (Kernel) といい、
の要素
で移した全体を
の 像(Image) と言います。
は
の、
は
の(線形)部分空間です。
さて、サイクルとは境界を取ると消えるものだったので、その全体は境界写像の 核 です。こうして 1次・2次 サイクル群 が得られます。
バウンダリは一つ上のチェインの境界のことだったので、その全体は上からくる境界写像の 像 (Image) ということになります。こうして 0次・1次 バウンダリ群 が得られます。
便宜的に 0次境界写像 をゼロ写像として、 0次サイクル群 は
とします(ゼロ写像の核は全体)。2次より上のチェイン群はないので 2次バウンダリ群 はゼロベクトル空間
とします(ゼロ写像の像はゼロ)。すると各次元でベクトル空間と部分空間が与えられ、次元間で境界写像によって移りあうような列が得られます:
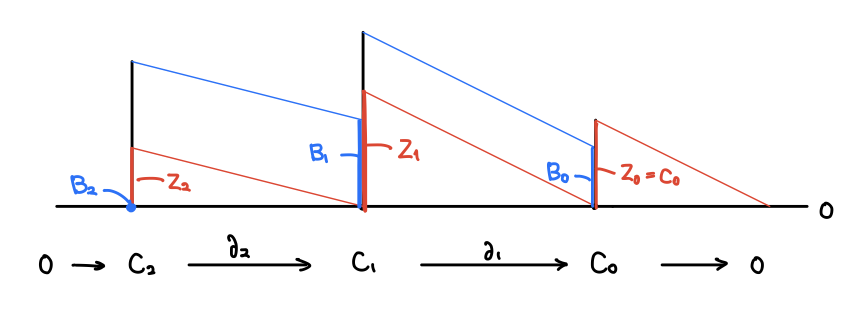
このようなベクトル空間と線形写像の列を チェイン複体 と言います。
商としてのホモロジー群
さて、考えたいのは バウンダリ群とサイクル群の差 でした。しかし単に集合として差をとってしまうと、ベクトル空間にならず上手く扱えません。そこでバウンダリ群によるサイクル群の商ベクトル空間を考えます。
各次元におけるこの商ベクトル空間を 0次・1次・2次 ホモロジー群 と言います。 (やっとホモロジー群が定義できた…!)
商ベクトル空間については慣れていない方も多いと思うので簡単に説明しておきます。ベクトル空間 とその部分空間
に対し、商ベクトル空間
は、
の要素のうち
成分を無視して得られるベクトル空間で、その次元は
となります。
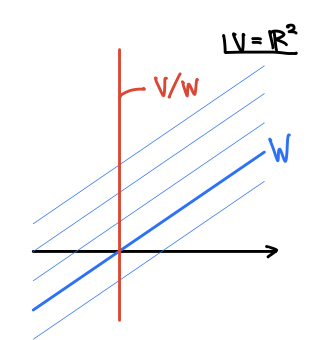
において
と独立な補空間を考え、そこへの射影が
だと考えても良いでしょう。
まとめ
- 曲面を三角形分割に対し、三角形の点・辺・面を基底とするベクトル空間としてチェイン群
を作る。
- 点・辺・面の境界の対応を見ることで、チェイン群の間の線形写像である境界写像
を定める。
- 各次元
について、
の核を
次サイクル群
、
の像を
次バウンダリ群
とする。
- 商ベクトル空間 H_n = Z_n / B_n を
次ホモロジー群と定める。
この定式化の下で「曲面の一部分の境界でないキリトリ線を調べる」という問題は、「曲面の1次ホモロジー群を調べる」という 代数的な問題 へと置き換えることができました!
はじめて見た方はとても複雑なことをしているように見えると思います。ホモロジーは「商を取る」という操作によって、曲面の三角形分割に依存する情報を消し、曲面そのものが持っている位相的な構造だけを取り出せるようにしています。私たちは位相不変量を知ろうとしているので、曲面の三角形分割の仕方に依存する情報は最終的には捨ててしまうのです!
ホモロジー群の計算(行列の基本変形)
さて、線形代数まで問題を落とせれば後は解くだけです。 球面の場合、各チェイン群の基底が境界写像でどこへ写っているかを描くと次のようになります:

まるでニューラルネットワーク図ですね(ただしこのニューラルネットワークは二つ進むとゼロになってしまうので役に立ちません)。これを上手く整理して各写像の核と像を求めたい。そこで使うのが行列の基本変形です。
行列の基本変形とは、行基本変形:
- 第 i 行 を a 倍する (a ≠ 0)
- 第 i 行 の a 倍を第 i 行に加える (a: 任意)
- 第 i 行 と 第 j 行 を交換する
とそれに対応する列基本変形を行列に施す操作のことでした。
球面における2次境界写像 の行列を基本変形すると次のようになります:

行基本変形は正則行列を左から、列基本変形は正則行列を右からかけることに対応しています。行列 から基本変形によって
が得られたとすると、正則行列
によって:
とあらわせます。行列表示とは線形写像によって基底がどこへ移るかの対応を並べたものだったので、上の式をベクトル空間と線形写像の言葉で言い直せば、始域の基底を で、終域の基底を
で変換すると、その行列表示が
になるということです。
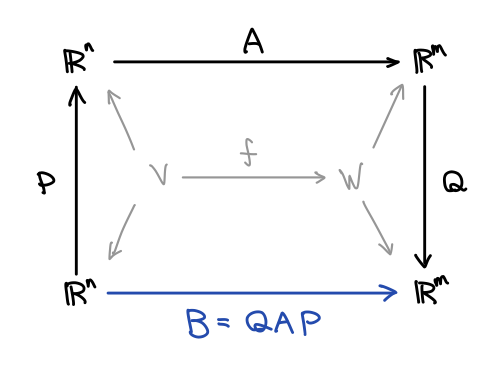
の例に戻ると、
と
の基底(三角形分割の面と辺)を線形結合によって組み替えることで、境界写像が右側の行列に書き直されます。このとき像は新しい基底で
に対応するチェインの行き先で、核は
に対応するチェインで張られる空間となります。特に
です。
同様に1次境界写像 の行列も基本変形すると:
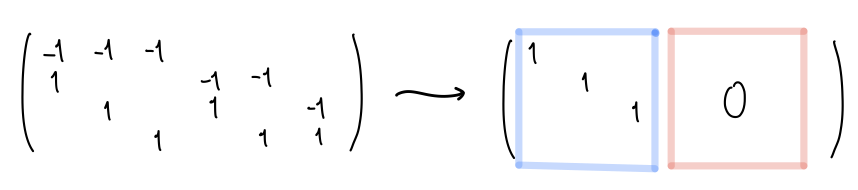
これより です。
新しく取り直した基底によってチェイン複体を見てみると:
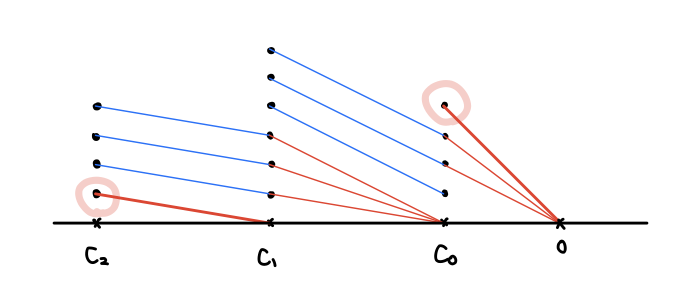
スッキリしましたね! これを見るとバウンダリがサイクルに含まれていることも、バウンダリのバウンダリがゼロであることも一目瞭然だと思います。
さて、注目したいのは「バウンダリでないサイクル」でした。この図を見ると と
にそれが一つずつあり、
にはないことが分かります。この差はサイクル群におけるバウンダリ群の補空間の基底なので、(その剰余類が)ホモロジー群の基底となります。つまり 2次・0次 ホモロジー群
は 1 次元で、
は 0 次元であるということです。
という事実は、まさしく球面には「曲面の一部分でないようなキリトリ線はない」という事実の現れです。
の意味は後で触れることにして、トーラスのホモロジー群を見て見ましょう。
トーラスの三角形分割では、頂点が 9 つ、辺が 27 個、面が 18 個あるので、それぞれチェイン群は 0 次から順に 9 次元、27 次元、 18 次元のベクトル空間です(ただの数の並びなので怖がらないで下さい)。それぞれの境界写像を行列表示し、基本変形することで複体は次のようになります:
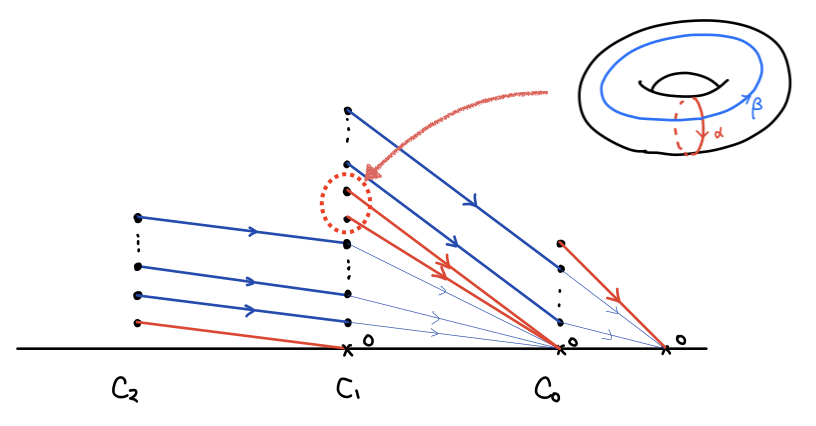
先ほどと決定的に違うのは にバウンダリでないサイクルの基底が二つあるということです。
が 2 次元だということです!このホモロジー群の基底に対応するサイクルが、トーラスをグルッと一周するサイクルと、縦にクルッと一周するサイクルです。
さて、球面もトーラスも は共に 1 次元でした。
このことは:
: 曲面は連結である
: 曲面は向きづけ可能である
を表しています。
簡単に説明すると、 においては全ての点がサイクルであり、
ということはどの二つの点の差も1次チェインの境界になっているということで、この 1次チェイン の辺を辿ることでそこへ到れる、つまり曲面が(弧状)連結だということを意味しています。
については、
だったので、これは
ということです。2次チェインがサイクルであるということは、その境界を取ると隣り合う二つの面で共有されている辺の成分が全てが打ち消し合うということなので、対応する曲面は閉曲面そのもので、全ての面で互いに同調する向きが取れるということです。
以上をまとめると、曲面を三角形に分割して、分割に応じたチェイン複体を構成し、ホモロジー群の構造を調べることで、
- 曲面の連結性
- 曲面の連結性を壊さないキリトリ線の個数
- 曲面の向きづけ可能性
といった位相不変な性質が一挙に分かってしまうのです。 すごい!
オイラー数の正体
前回紹介した曲面たちの位相不変な性質をまとめた表です:
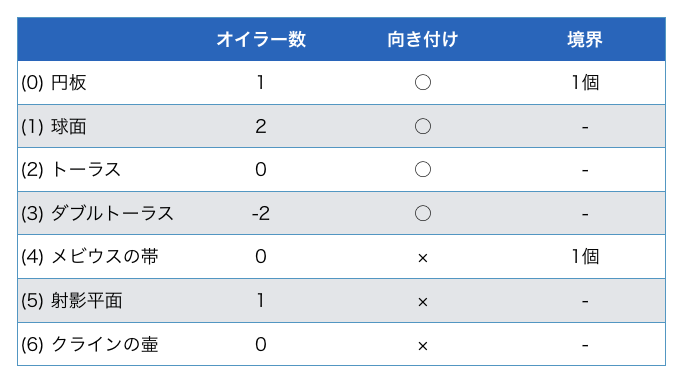
これらの三角形分割を取ってホモロジー群を計算したものが以下の通りです:
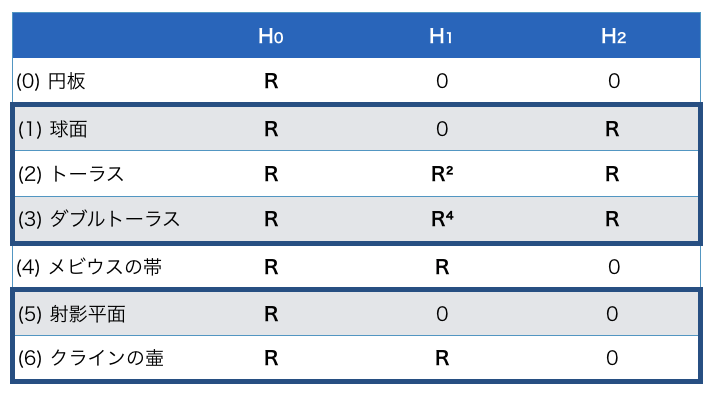
「閉曲面の分類定理」によれば閉曲面は向き付け可能性とオイラー数で完全に分類されるのでした。まず向き付け可能性は H_2 が R か 0 かで判定できます。オイラー数はというと、実は、
で与えられるのです!(確認してみて下さい) 第1回でオイラー数は、
(頂点の個数) - (辺の個数) + (面の個数)
として導入しました。チェイン群は、これらの個数に応じたベクトル空間だったので、
と一致します。先ほどのチェイン複体の図を見ると、隣り合う次元の差においてホモロジー群の次元が余って出て来ることが分かります:
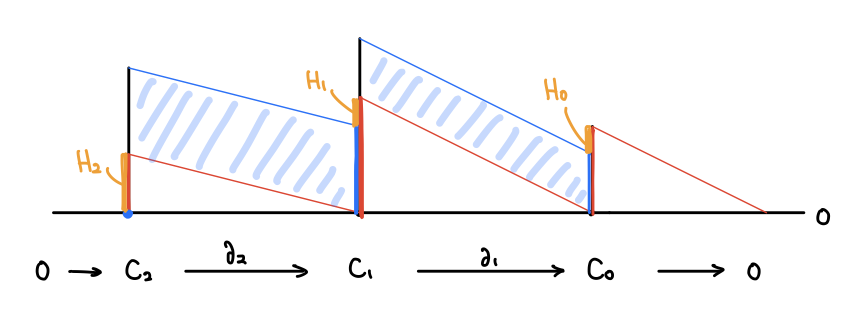
オイラー数はホモロジー群の次元の交代和4だったのです!
これだけだと、簡単に計算できるものをわざわざ計算の難しいもので置き換えただけに見えるかもしれません。しかし曲面の分割の仕方には色々なやり方があるのに対して、ホモロジー群の構造は位相不変なのです。このことを証明するのが代数トポロジーの第一関門となりますが、それを認めれば、位相不変なホモロジー群から取り出せるオイラー数もまた位相不変だと分かります。
以上より、オイラー数の正体と共に、閉曲面の分類に必要な情報は全てホモロジー群から得られるということが分かりました!
ホモロジー群可視化ツールでっち上げたぞ💪 pic.twitter.com/TaWT9H3oZQ
— さのたけと (@taketo1024) 2017年11月28日
今回の記事に向けて、ホモロジー群を計算して可視化するツールを作りました。元々「数学とコンピュータ」 Advent Calendar を作ったときはこれを解説するつもりでいたのですが、ホモロジー群の説明に加えて実装の解説まで入れると詰め込みすぎなので、それはまたの機会とさせて下さい🙇
より高い視点から 〜 圏論の扉を開けてみる
第一回で「トポロジーでは同相写像で移り合う図形は同じと見なし、それによって変わらない性質を調べる」と書きました。ユークリッド幾何学の合同変換・相似変換に対して同相写像はあまりに自由度が高く、その下で図形を調べるのは手のつけようがなさそうでした。
そこで図形のホモロジー群という代数的にカチッと構造の決まる対象へと移したのでした。ホモロジーという手段を使って、幾何的な対象を代数的な対象に変換した訳です。このことを圏論の言葉では、
ホモロジー関手は、位相空間の圏からベクトル空間の圏への関手である。
と言います。「圏と関手」が強いのは、単に対象を別の対象へ移すだけでなく、対象間の関係性も一緒に移してしまうところです。つまり位相空間の間の連続写像(同相写像)をベクトル空間の間の線形写像(線形同型写像)に移してしまうのです。
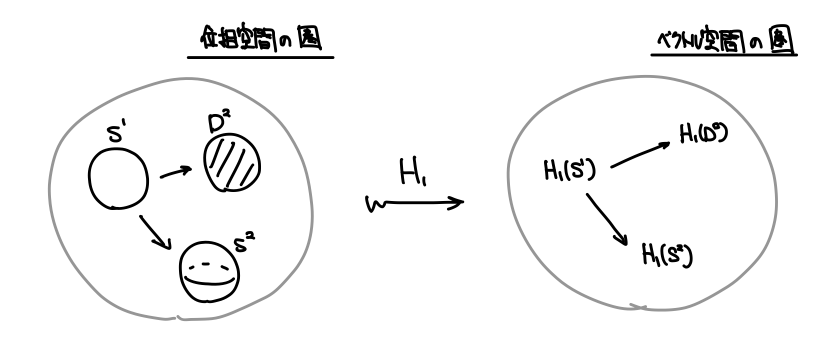
位相空間の圏で「同じ」ものが、ベクトル空間の圏でも「同じ」ものに移ってくれる。二つの図形が同相かどうかの判別は難しいですが、ホモロジー群がベクトル空間としての同型かはずっと簡単です。
このように現代数学では、関手を使って圏を丸ごと扱いやすい圏に移すことをよくします。このとき移った先で得られる情報が、元の圏の情報をどれだけ復元できるかというのは重要な問題です。閉曲面に関しては、ホモロジー関手は元の対象を完全に復元できる「十分いい」関手だった訳です。次元が上がると状況は絶望的に複雑になります5。
最後に
3回に渡って「トポロジーとは?」から「ホモロジー群の構成」まで書きました。トポロジーという言葉を初めて聞いた方や、数学専攻を志している人にとって興味を持つきっかけになれば幸いです。
まだホモロジー完全系列やホモロジーとコホモロジーのポアンカレ双対性など面白い話はたくさんあるので、追って記事を書きたいと思います。
ひとまずここまで読んで頂きありがとうございます。
メリークリスマス&よいお年を🎉
参考図書
数学専攻でない人がトポロジーに入門するにはこちらがオススメです。特別な前提知識なく読めると思います(恐らく高校生でも)。

- 作者: 瀬山士郎
- 出版社/メーカー: 日本評論社
- 発売日: 2003/11/01
- メディア: 単行本
- 購入: 4人 クリック: 150回
- この商品を含むブログ (9件) を見る
こちらはもう少し進んだ内容で、行列を使った具体的な計算やホモロジー群の位相不変性なども扱っています。

- 作者: 田中利史・村上斉
- 出版社/メーカー: サイエンス社
- 発売日: 2005/09/25
- メディア: 雑誌
- この商品を含むブログを見る
こちらは古典的なトポロジー(単体的複体のホモロジー群・基本群)の入門書です。

- 作者: 田村一郎
- 出版社/メーカー: 岩波書店
- 発売日: 2015/08/11
- メディア: オンデマンド (ペーパーバック)
- この商品を含むブログを見る
-
“In these days the angel of topology and the devil of abstract algebra fight for the soul of each individual mathematical domain.” Weyl, Hermann (1939), “Invariants”, Duke Mathematical Journal↩
-
補足↩
-
多くのトポロジーの入門書では整数係数でチェイン複体を構成します。その場合チェイン群はベクトル空間ではなく加群となります(係数環が体であるような加群を特にベクトル空間という)。しかし構成方法は変わらないので、この記事では R (または Q)係数を考えチェイン群はベクトル空間であるとします。↩
-
補足↩
-
ポアンカレははじめ、1次元・2次元で言えるのと同様に3次元についても「ホモロジー群が3次元球面 S3 と同型になる閉多様体は、S3 と同相だろう」と予想しました。その後自ら反例となる「ポアンカレのホモロジー球面」を構成します。こうして次に「ホモトピー群が S3 と同型である閉多様体は、S3 と同相だろうか?」という問いを立てました。これが「ポアンカレ予想」で、提唱された 1904 年から約 100 年のときを経て 2002 年にロシア人の数学者 G・ペレルマン によって肯定的に解決されました。↩