トポロジーへの招待 〜 2. 切り貼りで作る色々な曲面
この記事は 数学とコンピュータⅡ Advent Calendar 18日目の記事です。
こんにちは、佐野です。前回の記事をたくさんの方に読んで頂けたようで嬉しいです。元々は 3 回で書き切るつもりでいたのですが、詰め込み過ぎてもよくないしちゃんと書きたい話はもっとあるので Advent Calendar 期間が過ぎてもシリーズを続けることにしました👍
前回の復習
トポロジーは同相写像で移り合う図形を「同じ」と見なし、その同一視の下で変わらない図形の性質(位相不変量)を調べる分野でした。位相不変量の例として、多面体の頂点・辺・面の個数から決まるオイラー数を紹介しました。
今回は球面やトーラスなどの身近な曲面から、日常では決して見ることのない不思議な曲面まで色々と観察し、それらを区別するにはどうすればいいか考えていきましょう。
曲面いろいろ
0) 円板 D2
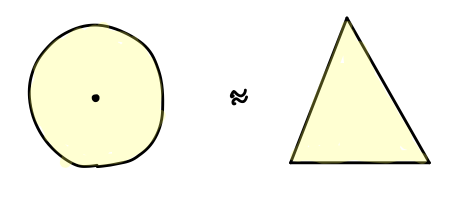
曲面と呼ぶにはつまらない例ですが、数学ではまず自明な例から始めことになっているので紹介します。円板 (disk)1 は三角形(内部も含む)と同相であり、円周 S1 がその境界です(肩に乗っている数がその図形の次元を現しています)。オイラー数は三角形の辺・頂点・面の数を数えて V - E + F = 1 です。
1) 球面 S2
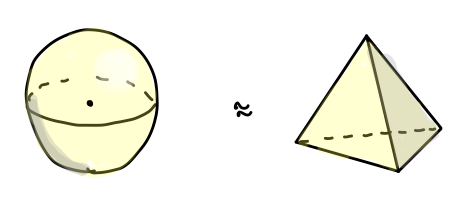
球面 (sphere) はトポロジーにおける最も基本的な閉曲面2です。前回、正多面体が球面と同相であることを述べましたが、トポロジカルには「穴の空いていない多面体」は全て球面です。そのオイラー数は等しく 2 となるのでした。
この先出てくる曲面の説明のためにも、多面体を使わずに紙を切り貼りして曲面を作る方法を紹介しましょう。下の長方形は自由に伸縮できる理想的な素材でできていると考えて下さい。がま口財布を閉じるように長方形の辺 a と a'、b と b' を張り合わせると球面ができます。
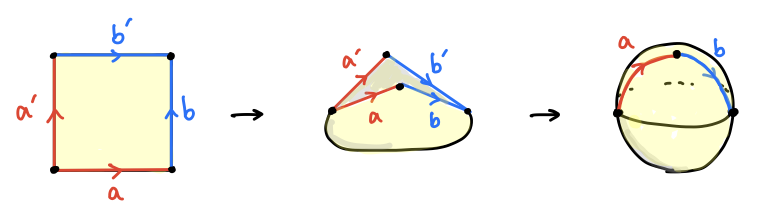
貼り合わせて作った図形は、頂点の数は 4 個のうち 2 個がくっついたので V = 3、辺は 4 個のうち 2 つずつペアになったので E = 2、面は一つだけなので F = 1 となり、この場合も V - E - F = 2 です。
別の作り方もあります。風呂敷で包むようにして長方形の周を一点に潰してしまいます3。
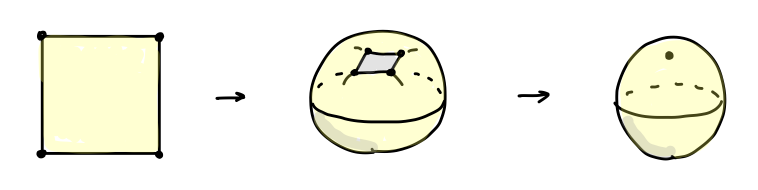
この場合、頂点は一つになるので V = 1、辺はなくなってしまったので E = 0、面は F = 1 なのでやはり V - E + F = 2 です。図画工作みたいで楽しいでしょ😙
2) トーラス T2
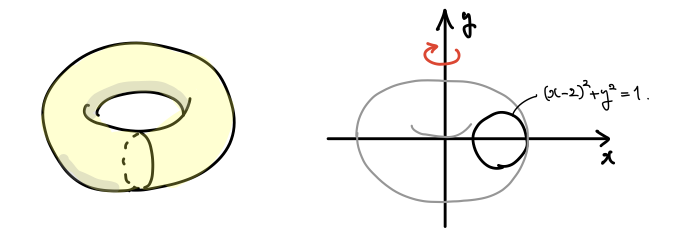
トーラスはドーナッツの表面に現れる閉曲面です。トポロジーでは球面の次に基本的な図形として出てきます。ユークリッド空間では、xy 平面上に y 軸から離れたところに円周をおいて y 軸に関して回転させることで得られます。
前回、多面体でトーラスを作って オイラー数 = 0 であることを見ました。これも長方形の切り貼りで作ることができます。今回は長方形で向かい合う辺の組み(a, a'), (b, b') を貼り合わせます。
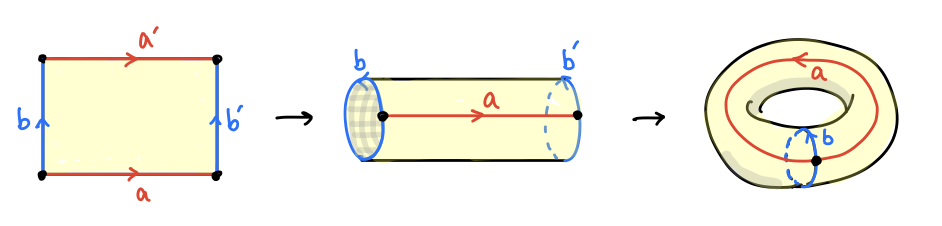
頂点は全て同一視されるので V = 1、あとは E = 2, F = 1 なので、やはり V - E + F = 0 です。
余談ですがファミコン/スーファミ世代にとってトーラスはお馴染みの空間です。RPG の世界では、マップ上で右端を過ぎると左端から出て、上端を過ぎると下端に出るので、境界で向かい合う辺が貼り合っていることになります。これは紛れもなくトーラスです。RPG の世界の「地球」は、トポロジカルにはドーナッツ形をしていることが分かります4。
3) ダブルトーラス T2#T2

ダブルトーラスはその名の通りトーラスを二個繋げた閉曲面です。これも前回、穴が二つ空いた多面体からオイラー数が -2 であることを見ました。実はこれも一枚の紙の貼り合わせで作れます。八角形の周上で、辺を一つおきにペアにして貼り合わせるできます。
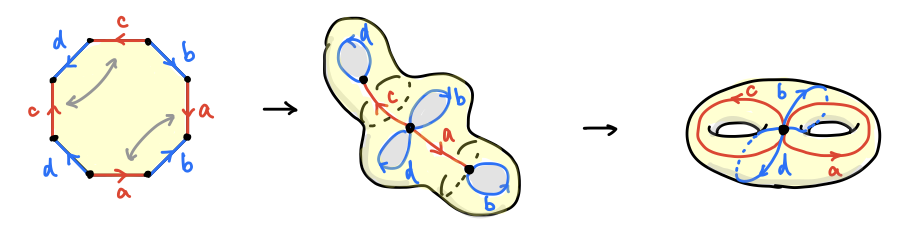
この作り方ビックリですよね。僕は図だけだと信じきれなかったので、粘土で作ってみたことがあります。
勤労感謝の日ってことで、八角形から種数2の閉曲面作るのやってみた。 pic.twitter.com/ghfRiZyZso
— さのたけと (@taketo1024) 2016年11月23日
さらにこのやり方で、好きな数だけ穴を空けた閉曲面が作れます。穴の数 g に対して、4g 角形の辺を一つおきに貼り合わせればいいのです。g = 3 の場合がこれです:
種数3にチャレンジ💪 pic.twitter.com/rfilvVVj6d
— さのたけと (@taketo1024) 2016年11月23日
穴が g 個空いた閉曲面のオイラー数は、頂点が一つで V = 1、辺は 4g 個あるものがペアになるので半分の E = 2g、面は F = 1 なので、オイラー数 2 - 2g となります。前回出した式が得られました!
こちらの CG動画 では 40角形 を貼り合わせて穴が 10 個あいた閉曲面を作っています(これを粘土でやるのはキツそう)。
4) メビウスの帯
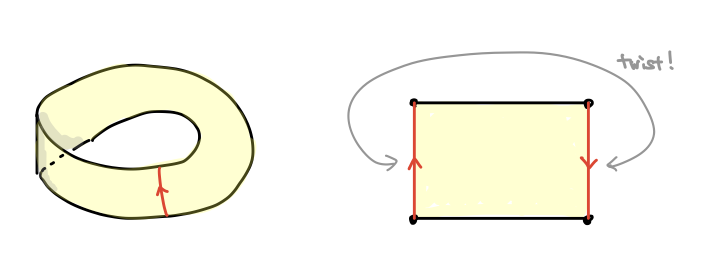
メビウスの帯を作ったことはありますか?なければ今、紙を帯状に切ってその両端を捻ってセロテープで貼り合わせて作ってみましょう。この図形は、中心線に沿ってグルッと一周するとスタート地点の裏側に着いてしまう 向き付け不可能5 な曲面です。

境界はどうなっているでしょう?指で帯のヘリをなぞってみると分かるように、一個の円周が二周巻きになったものが出てきます。オイラー数は 2 - 3 + 1 = 0 です。
ここからだんだん不思議なトポロジーの世界へ入って行きます👣
5) 射影平面 P2

長方形の向かい合う辺をトーラスの場合とは逆向きに貼り合わせてできる曲面が射影平面 (projective plane) です。これを実際に作ってみようとするとどうしても面がぶつかってできません。これは私たちが 3 次元空間で生きているからで、4 次元方向へ少しズラせば(!?) 面の交叉は回避できます。メビウスの帯を貼り合わせるのに平面から浮かせて 3 次元空間で行ったことと同じです。
右の図(交叉帽という)を見るときは、4 次元空間内の図形を 2 次元分落とした平面への影を見ていると考えましょう。交わっている部分はたまたま影が重なってそう見えているだけです。ただし交叉帽は射影平面を無理やりユークリッド空間に入れたときの姿なので、むしろ左の二つの展開図で理解した方が良いと思います。
もし RPG のマップが射影平面だったら、マップを一周して戻ってくるといつのまにか体が逆向きになってしまうでしょう。射影平面では全ての方向でメビウスの帯のような「裏返り」が起きます。なぜこんな訳の分からない図形を考えるのでしょう。
射影平面は球面の対蹠点を同一視した空間と見ることができます。この空間は、球面の中心を通る直線のパラメータ空間になっています。球面の前に平面を置いてこれをスクリーンと考えると、射影平面はこのスクリーンと、スクリーンとは交わらない「無限遠直線上の点たち」からなっています。
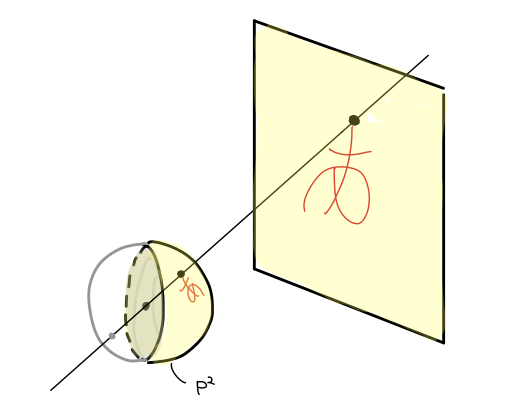
ユークリッド平面上の図形をこのスクリーンに映った影だと見ると、スクリーンを置く位置を変えることで平面上で交わる 2 直線の交点を「無限遠に飛ばして」平行にしてしまったり、放物線の「無限遠の交点」を手前に持ってきて楕円に変えることができたりします。ユークリッド平面上では魔法のように見える操作が射影平面では当たり前にできて、ユークリッド幾何学の範疇では複雑な定理も射影幾何学6では鮮やかに証明できてしまったりするのです。
射影平面のオイラー数は 2 - 2 + 1 = 1 です。
6) クラインの壷
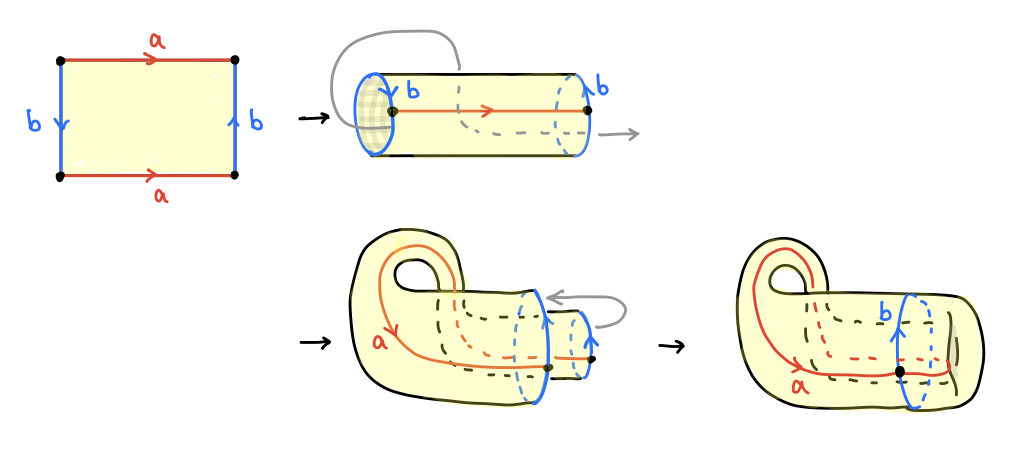
長方形の向かい合う辺の組のうち、一つは同じ向きに、もう一つは逆向きに貼り合わせた曲面がクラインの壷 (Klein bottle)です。これも向き付け不可能な曲面で、 3 次元空間の中で作ろうとすると面がぶつかってしまいますが、4 次元空間の中で面が交わらないように辺を貼り合わせることで壷のような形の図形が得られます。
これも向き付け不可能で、オイラー数は 1 - 2 + 1 = 0 です。
一旦まとめ
これらの曲面とその性質をまとめます:
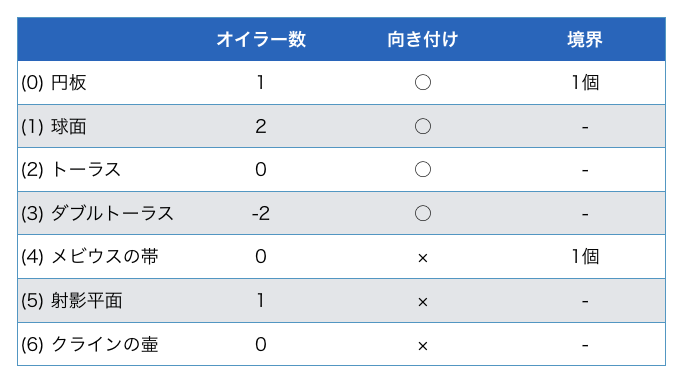
これらの図形はどれも互いに同相ではありません。オイラー数だけを見ると重複しているものがありますが、三つの項目の組み合わせは一意です。実はこれは一般に言えることで、コンパクトな曲面は全てこの三つで分類できます。特に閉曲面(コンパクトで境界のない曲面)については、オイラー数と向きづけ可能性だけで分類できます。これが「閉曲面の分類定理」です。
とはいえ向きづけ可能性はオイラー数と比べて抽象的で捉えどころがない感じがします。何か複雑な多面体が与えられたとき、それが向きづけ可能かどうかは判定できるのでしょうか?
前回から残している疑問もあります:
- オイラー数 V - E + F は一体どこから出て来たのか?
- なぜこの量は位相不変となるのか?
この先これらの疑問への答えを得ることを目指し、図形の構造を取り出す具体的な方法を探って行きましょう。
今度は曲面をハサミで切ってみよう
まずは球面とトーラスをどう区別するかから考えてみましょう。
次は「ジョルダンの閉曲線定理」です:
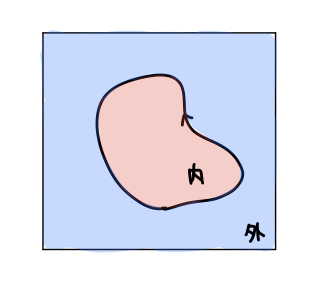
平面内の単純閉曲線は、平面を内側と外側の二つの領域に分ける。
あまりに当たり前のようで「こんなものが定理になるのか?」とすら感じられます。しかしその証明は難しく7、20世紀初頭にようやく得られました。何せ閉曲線の形が全く具体的に与えられていないのですから(至るところ滑らかでない病的な曲線かも知れません)。
いま注目したいのは、この「当たり前」は球面についてはそのまま成り立つが、トーラスについては成り立たないということです!球面はどんな風に切っても二つの部分に分かれてしまうが、トーラスにはそうならない切り方があります。
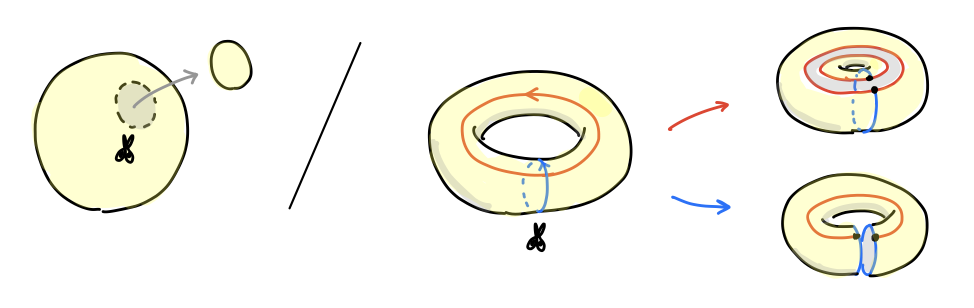
(他の曲面に対しても連結性を保つような切り方が色々とあります。展開図を見ながら試してみてください、特にメビウスの帯は楽しい!)
これは曲面の繋がり方(位相 = トポロジー)を区別する性質と言えそうです。 それでは二つに分かれる切り方と分かれない(連結性を保つ)切り方の違いはなんでしょう?
二つに分かれる切り取り線は、曲面の一部分であった二つの曲面の境界となっています。曲面の一部分の境界として現れるようなキリトリ線に沿って切れば、曲面は二つに分かれる訳です。逆に曲面の一部分の境界でないようなキリトリ線に沿って切れば、連結性は保たれることになります。
連結性を保つような切り方はどれぐらいあるのでしょうか?この情報を持っているのが図形の 1次ホモロジー群 です。 次回、曲面のホモロジー群を定義し、閉曲面がホモロジー群によって完全に分類されることを見ていきましょう!
参考図書
前回紹介した二つの本には「閉曲面の分類定理」が載っています。多角形から閉曲面を作る議論を一般に行い、曲面を何度も切ったり貼ったりすることで標準形に変形するという議論をします。

- 作者: 瀬山士郎
- 出版社/メーカー: 日本評論社
- 発売日: 2003/11/01
- メディア: 単行本
- 購入: 4人 クリック: 150回
- この商品を含むブログ (9件) を見る

- 作者: 田村一郎
- 出版社/メーカー: 岩波書店
- 発売日: 2015/08/11
- メディア: オンデマンド (ペーパーバック)
- この商品を含むブログを見る
面白いトポロジーの絵をもっと見たいという方にはコチラがオススメです。中世の解剖学書か?と思えるような楽しい(グロテスクな)絵がたくさん出てきます。

トポロジーの絵本 新装版 (シュプリンガー数学リーディングス)
- 作者: G.K.フランシス,笠原晧司,宮崎興二
- 出版社/メーカー: シュプリンガー・フェアラーク東京
- 発売日: 2005/12/01
- メディア: 単行本
- 購入: 1人 クリック: 26回
- この商品を含むブログ (7件) を見る
少し触れた射影幾何学の入門書はこちらがオススメです。

- 作者: 西山享,飯高茂,中村滋,岡部恒治,桑田孝泰
- 出版社/メーカー: 共立出版
- 発売日: 2013/11/09
- メディア: 単行本
- この商品を含むブログ (2件) を見る
-
単に「円」というと内部を含むのか含まないのかハッキリしないので、内部を含む場合は 円板 (disk) といい、含まない場合は 円周 (circle) と言います。↩
-
コンパクトで境界のない曲面を 閉曲面 と言います。この 閉 は閉集合の 閉 とは別です。例えば円板は閉曲面ではありませんが(円周がその境界なので)ユークリッド空間の中では閉集合です。↩
-
「こんな貼り合わせ方アリなの?」と思われたかも知れません。この作り方で得られる図形は多面体ではなく、より一般に 胞体 と呼ばれるものです。胞体についても多面体と同じやり方でオイラー数が求められるのは、それぞれのホモロジー群が同型であるという事実に依っています。↩
-
FF4 で月から地球(?)に戻って来るときに球体のようなものが見えた気がするのですが、球面とトーラスは同相でないのでちょっと不思議です。↩
-
向き (orientation) は 方向 (direction) とは別の概念です。3次元空間内の曲面の向きとは、その法線(曲面に直行する直線)の方向のことで、つまりは曲面の表裏のことです。より一般の状況での向きの定義はもっと難しくなります。↩
-
このような変換を射影変換といい、射影変換で不変な不変量を調べるのが射影幾何学です。↩
-
まさしくその証明にホモロジー理論を使います。従ってホモロジー理論の導入にジョルダンの閉曲線定理を使うのは循環論法になりますが、ここでは日常的な「当たり前」の感覚に頼って話を進めることにします。↩