トポロジーへの招待 〜 3. ホモロジー群の構成とオイラー数の正体

最近では、トポロジーの天使と抽象代数学の悪魔との葛藤が、すべての数学の研究で起きている。¹

20世紀の数学者ヘルマン・ワイルの言葉です。過去2回の記事を読んでくれた方は「トポロジー楽しそう！」と感じてくれたことと思います。これまでは「トポロジーの天使」の紹介でした。

今回は「抽象代数学の悪魔」の話です。

…と言っても「悪魔の力」のほんの一部を紹介する程度です。図形の位相不変量が具体的に計算できる面白さをお見せしたい。天使と悪魔の二面性こそがトポロジーの（あるいは数学の）の面白さだと思うので、それが共有できたら幸いです😙

この記事は 数学とコンピュータ Advent Calendar 25日目の記事です。

1. 座標も補助線も使わない「やわらかい幾何学」
2. 切り貼りで作る色々な曲面
3. ホモロジー群とオイラー数の正体 ←

前回の復習

前回は球面・トーラスなどのお馴染みの曲面から、射影平面・クラインの壷など日常では見ることのできない曲面まで色々と紹介し、これらの閉曲面がオイラー数と向きづけ可能性だけで分類できることを述べました。

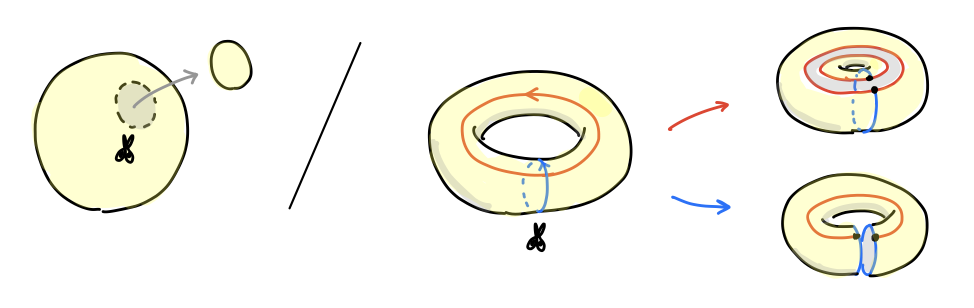
閉曲面を分類するための指針として「キリトリ線に沿って曲面を切って、曲面が二つに分かれないものはどれだけあるか？」を考察しました。今回はこれらの位相不変量をアルゴリズミックに取り出す方法として（単体複体の）ホモロジー群 を導入します。

線形代数（ベクトルと行列）の基本的な知識を前提としますが、適宜補足を入れてあるのでついてきて下さい👍

チェイン複体の構成

1次チェイン

「曲面の一部分の境界でないキリトリ線」 がどれだけあるかを調べたい。曲面上の曲線の取り方は無限にあるので、このままだと掴み所がありません。そこで曲面を CG のポリゴンメッシュのように三角形で分割して、その辺に沿った曲線を考えることにします。こうすれば考えうる曲線は有限個になるので、組み合わせ的に問題が解決できそうです。

球面は四面体の境界とし、トーラスは図のように 18個 の三角形で分割します²。

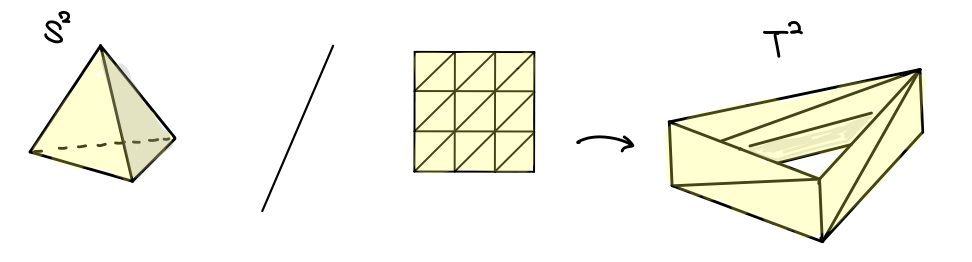
これらの辺上の曲線を表示するために、各辺に名前をつけて向きを定め、曲線を足し算の形で現します（逆向きに進む場合は -1 とする）。

このように足し算の形で表した辺の組を 1次チェイン と呼ぶことにします（1次は曲線の次元）。

1次サイクル

考えたい曲面上のキリトリ線は、グルッと一周して元に戻ってくる閉曲線です。各辺 に対して、始点を -1、終点を +1 で表すことにし、辺の 境界 を、

のように書くことにします。

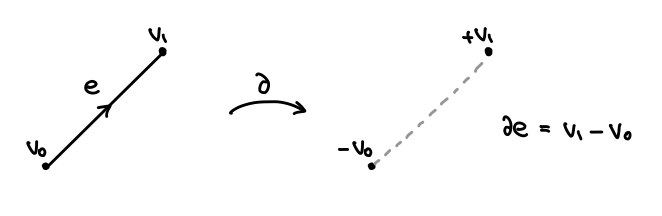
チェイン c を表す曲線が閉じているためには、すべての始点と終点がペアになるような辺の組があればいいので、

が求める条件です。このように1次チェインであって境界が消えているものを 1次サイクル と呼びます。

2次チェインと1次バウンダリ

次に「曲面の一部分」を組み合わせ的に表示します。曲面を構成する三角形のすべての面にグルッと一周する向きを定めておきます。

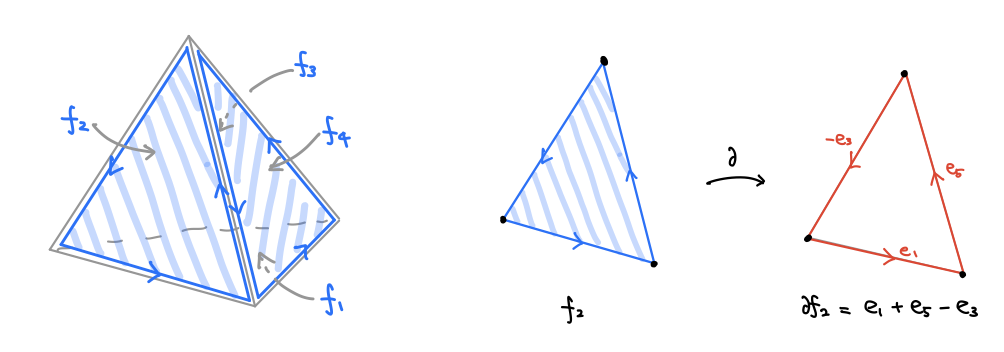
辺の境界として両端の点が出てきたように、今度は面の境界として辺が出てきます。 のように、二つの面が一つの辺を共有していて辺の向きが逆になっている場合、合わせて一つの曲面だと考えることができます。こうして三角形の面たちを足し算で閉曲面の一部（あるいは閉曲面そのもの）表したものを 2次チェイン と呼びます。

2次チェインの境界として現れる 1次チェインを、1次バウンダリと呼びます。「曲面の一部分の境界でないキリトリ線」は「1次サイクルであって、1次バウンダリでないもの」と言い換えられるようになりました。

ここで重要な事実として「1次バウンダリは、1次サイクルである」ということがあります。2次チェインの境界として現れる1次チェインは、もう一度境界を取ると消えてしまうのです。

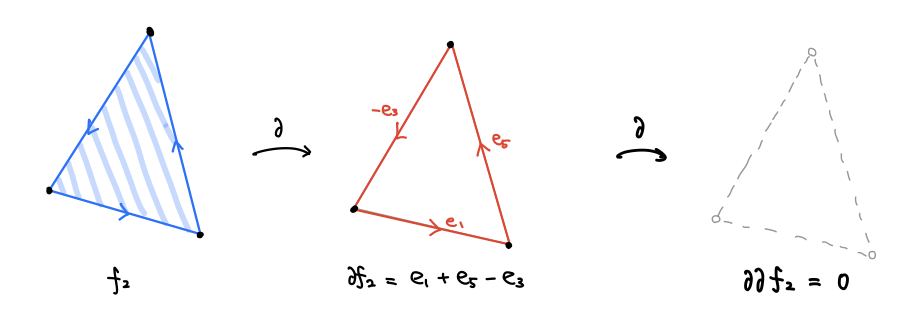
チェイン・サイクル・バウンダリの包含関係は：

{バウンダリ} ⊂ {サイクル} ⊂ {チェイン}

となっています。私たちの問題は「1次バウンダリと1次サイクルの差がどれだけあるかを調べたい」ということだと分かりました。球面とトーラスの場合だと、

• 球面上の1次サイクルは、2次チェインの境界として現れるものしかない
• トーラス上の1次サイクルには、2次チェインの境界でないものがある

となっているのでした。

線形代数で定式化

チェインだのサイクルだの出てきてゴチャゴチャしたと思うので、上記の話を全て線形代数で定式化し直しましょう。まず曲面に三角形分割に対し、その点・辺・面に全て向きを定め、それらを基底とするベクトル空間³を考えます。これを下から順に 0次・1次・2次 チェイン群 と呼びます。

先ほど足し算で表示した 1次 サイクルは、基底に関して成分表示することで辺の個数分の次元を持つベクトルとして表示することができます：

面に対してその境界の辺を取る操作を考えましたが、これは の基底である面の境界が 1 次チェイン群のどの要素に対応するかを見ることで、 から への線形写像を定めます。これを 2次 境界写像 と言います。

線形写像は始域と終域のベクトル空間の基底によって行列表示することができます。球面の場合の1次境界写像を行列表示は次のようになります。行列を見れば、例えば の境界は であることがわかります。

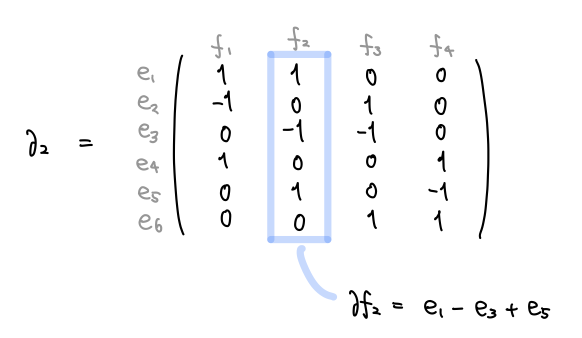
同様に、辺に対して境界の点を対応させる操作で から への線形写像が定まります。

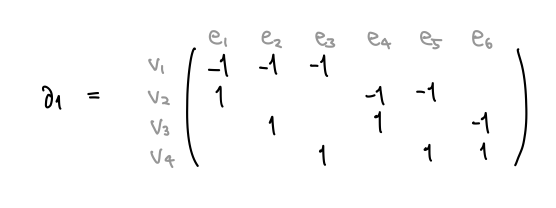
こうして曲面の三角形分割から、点・辺・面の個数だけの次元を持った 3 つのベクトル空間 チェイン群 と、その間で次数を落とす線形写像である 1次・2次 境界写像 を定義することができました。

サイクル（核）とバウンダリ（像）

（線形代数の一般論）線形写像 に対して、 によって に移ってしまう の要素全体を の 核 (Kernel) といい、 の要素 で移した全体を の 像(Image) と言います。 は の、 は の（線形）部分空間です。

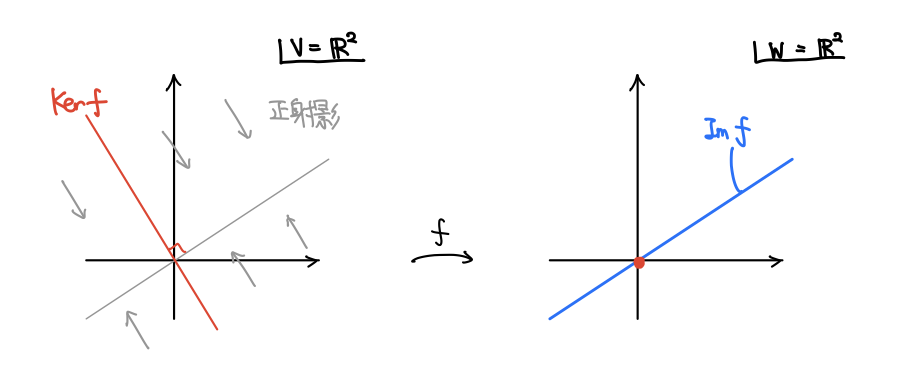
さて、サイクルとは境界を取ると消えるものだったので、その全体は境界写像の 核 です。こうして 1次・2次 サイクル群 が得られます。

バウンダリは一つ上のチェインの境界のことだったので、その全体は上からくる境界写像の 像 (Image) ということになります。こうして 0次・1次 バウンダリ群 が得られます。

便宜的に 0次境界写像 をゼロ写像として、 0次サイクル群 は とします（ゼロ写像の核は全体）。2次より上のチェイン群はないので 2次バウンダリ群 はゼロベクトル空間 とします（ゼロ写像の像はゼロ）。すると各次元でベクトル空間と部分空間が与えられ、次元間で境界写像によって移りあうような列が得られます：

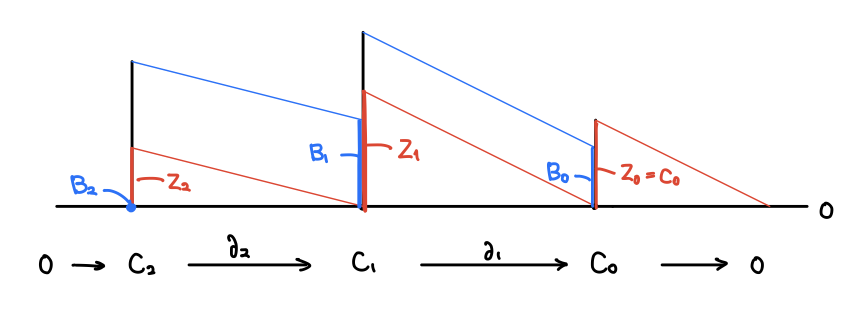
このようなベクトル空間と線形写像の列を チェイン複体 と言います。

商としてのホモロジー群

さて、考えたいのは バウンダリ群とサイクル群の差 でした。しかし単に集合として差をとってしまうと、ベクトル空間にならず上手く扱えません。そこでバウンダリ群によるサイクル群の商ベクトル空間を考えます。

各次元におけるこの商ベクトル空間を 0次・1次・2次 ホモロジー群 と言います。 （やっとホモロジー群が定義できた…！）

商ベクトル空間については慣れていない方も多いと思うので簡単に説明しておきます。ベクトル空間 とその部分空間 に対し、商ベクトル空間 は、 の要素のうち 成分を無視して得られるベクトル空間で、その次元は となります。

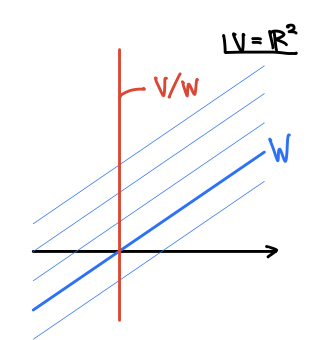
において と独立な補空間を考え、そこへの射影が だと考えても良いでしょう。

まとめ

• 曲面を三角形分割に対し、三角形の点・辺・面を基底とするベクトル空間としてチェイン群 を作る。
• 点・辺・面の境界の対応を見ることで、チェイン群の間の線形写像である境界写像 を定める。
• 各次元 について、
  • の核を 次サイクル群 、
  • の像を 次バウンダリ群 とする。
• 商ベクトル空間 H_n = Z_n / B_n を 次ホモロジー群と定める。

この定式化の下で「曲面の一部分の境界でないキリトリ線を調べる」という問題は、「曲面の1次ホモロジー群を調べる」という 代数的な問題 へと置き換えることができました！

はじめて見た方はとても複雑なことをしているように見えると思います。ホモロジーは「商を取る」という操作によって、曲面の三角形分割に依存する情報を消し、曲面そのものが持っている位相的な構造だけを取り出せるようにしています。私たちは位相不変量を知ろうとしているので、曲面の三角形分割の仕方に依存する情報は最終的には捨ててしまうのです！

ホモロジー群の計算（行列の基本変形）

さて、線形代数まで問題を落とせれば後は解くだけです。 球面の場合、各チェイン群の基底が境界写像でどこへ写っているかを描くと次のようになります：

まるでニューラルネットワーク図ですね（ただしこのニューラルネットワークは二つ進むとゼロになってしまうので役に立ちません）。これを上手く整理して各写像の核と像を求めたい。そこで使うのが行列の基本変形です。

行列の基本変形とは、行基本変形：

1. 第 i 行 を a 倍する (a ≠ 0)
2. 第 i 行 の a 倍を第 i 行に加える (a: 任意)
3. 第 i 行 と 第 j 行 を交換する

とそれに対応する列基本変形を行列に施す操作のことでした。 球面における2次境界写像 の行列を基本変形すると次のようになります：

行基本変形は正則行列を左から、列基本変形は正則行列を右からかけることに対応しています。行列 から基本変形によって が得られたとすると、正則行列 によって：

とあらわせます。行列表示とは線形写像によって基底がどこへ移るかの対応を並べたものだったので、上の式をベクトル空間と線形写像の言葉で言い直せば、始域の基底を で、終域の基底を で変換すると、その行列表示が になるということです。

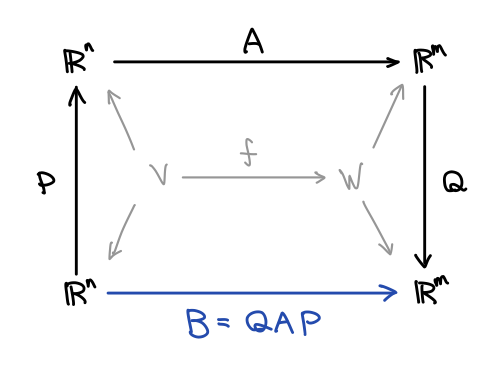
の例に戻ると、 と の基底（三角形分割の面と辺）を線形結合によって組み替えることで、境界写像が右側の行列に書き直されます。このとき像は新しい基底で に対応するチェインの行き先で、核は に対応するチェインで張られる空間となります。特に です。

同様に1次境界写像 の行列も基本変形すると：

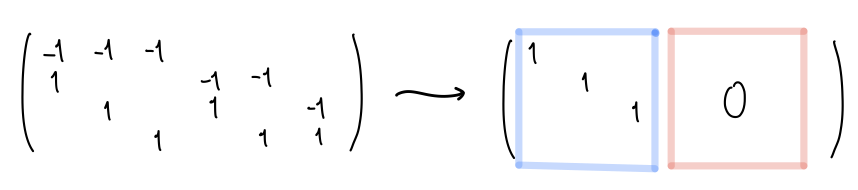
これより です。

新しく取り直した基底によってチェイン複体を見てみると：

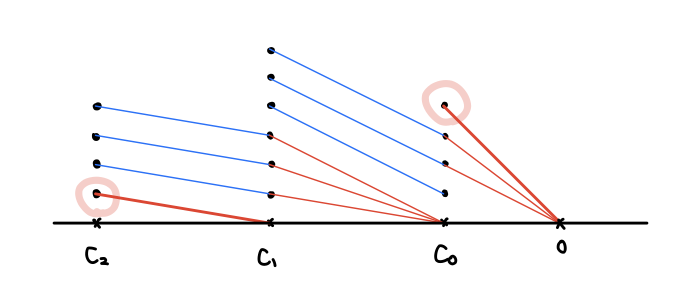
スッキリしましたね！ これを見るとバウンダリがサイクルに含まれていることも、バウンダリのバウンダリがゼロであることも一目瞭然だと思います。

さて、注目したいのは「バウンダリでないサイクル」でした。この図を見ると と にそれが一つずつあり、 にはないことが分かります。この差はサイクル群におけるバウンダリ群の補空間の基底なので、（その剰余類が）ホモロジー群の基底となります。つまり 2次・0次 ホモロジー群 は 1 次元で、 は 0 次元であるということです。

という事実は、まさしく球面には「曲面の一部分でないようなキリトリ線はない」という事実の現れです。 の意味は後で触れることにして、トーラスのホモロジー群を見て見ましょう。

トーラスの三角形分割では、頂点が 9 つ、辺が 27 個、面が 18 個あるので、それぞれチェイン群は 0 次から順に 9 次元、27 次元、 18 次元のベクトル空間です（ただの数の並びなので怖がらないで下さい）。それぞれの境界写像を行列表示し、基本変形することで複体は次のようになります：

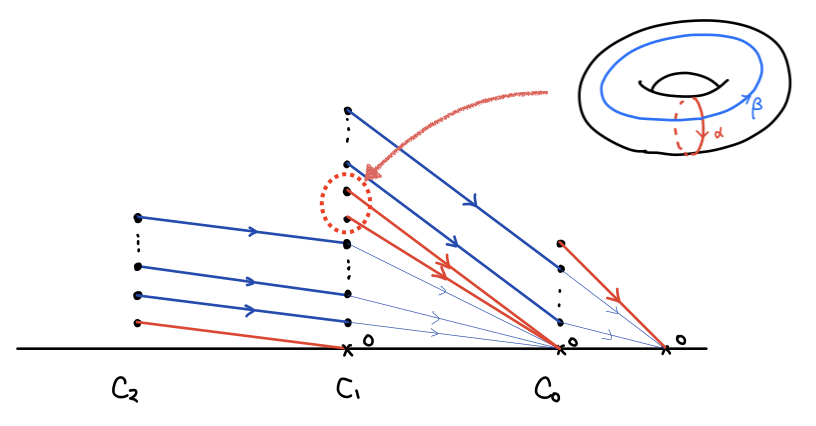
先ほどと決定的に違うのは にバウンダリでないサイクルの基底が二つあるということです。 が 2 次元だということです！このホモロジー群の基底に対応するサイクルが、トーラスをグルッと一周するサイクルと、縦にクルッと一周するサイクルです。

さて、球面もトーラスも は共に 1 次元でした。 このことは：

• : 曲面は連結である
• : 曲面は向きづけ可能である

を表しています。

簡単に説明すると、 においては全ての点がサイクルであり、 ということはどの二つの点の差も1次チェインの境界になっているということで、この 1次チェイン の辺を辿ることでそこへ到れる、つまり曲面が（弧状）連結だということを意味しています。

については、 だったので、これは ということです。2次チェインがサイクルであるということは、その境界を取ると隣り合う二つの面で共有されている辺の成分が全てが打ち消し合うということなので、対応する曲面は閉曲面そのもので、全ての面で互いに同調する向きが取れるということです。

以上をまとめると、曲面を三角形に分割して、分割に応じたチェイン複体を構成し、ホモロジー群の構造を調べることで、

• 曲面の連結性
• 曲面の連結性を壊さないキリトリ線の個数
• 曲面の向きづけ可能性

といった位相不変な性質が一挙に分かってしまうのです。 すごい！

オイラー数の正体

前回紹介した曲面たちの位相不変な性質をまとめた表です：

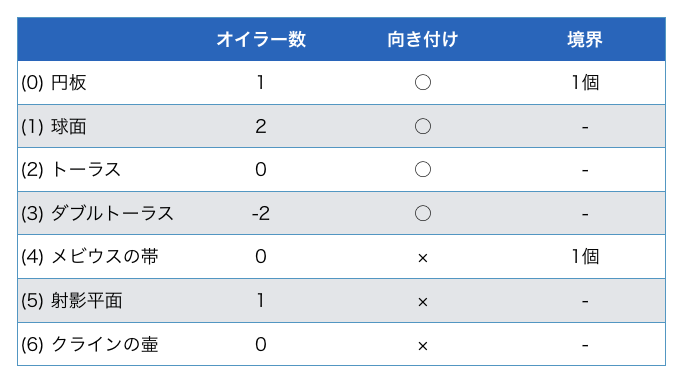
これらの三角形分割を取ってホモロジー群を計算したものが以下の通りです： 　　

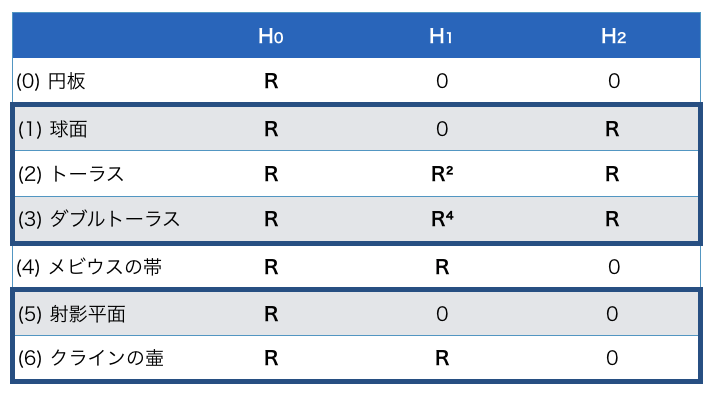
「閉曲面の分類定理」によれば閉曲面は向き付け可能性とオイラー数で完全に分類されるのでした。まず向き付け可能性は H_2 が R か 0 かで判定できます。オイラー数はというと、実は、

で与えられるのです！（確認してみて下さい） 第1回でオイラー数は、

(頂点の個数) - (辺の個数) + (面の個数)

として導入しました。チェイン群は、これらの個数に応じたベクトル空間だったので、

と一致します。先ほどのチェイン複体の図を見ると、隣り合う次元の差においてホモロジー群の次元が余って出て来ることが分かります：

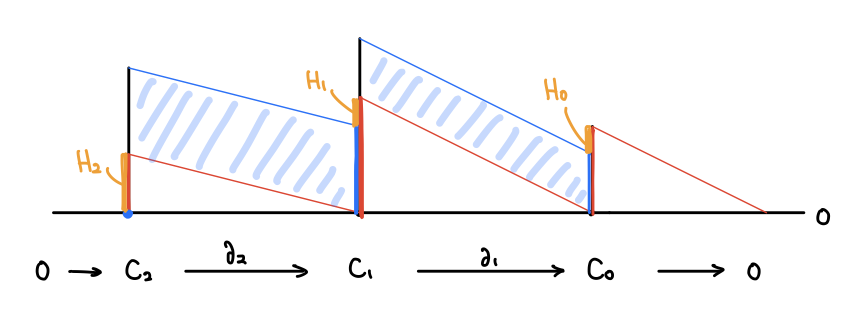
オイラー数はホモロジー群の次元の交代和⁴だったのです！

これだけだと、簡単に計算できるものをわざわざ計算の難しいもので置き換えただけに見えるかもしれません。しかし曲面の分割の仕方には色々なやり方があるのに対して、ホモロジー群の構造は位相不変なのです。このことを証明するのが代数トポロジーの第一関門となりますが、それを認めれば、位相不変なホモロジー群から取り出せるオイラー数もまた位相不変だと分かります。

以上より、オイラー数の正体と共に、閉曲面の分類に必要な情報は全てホモロジー群から得られるということが分かりました！

ホモロジー群可視化ツールでっち上げたぞ💪 pic.twitter.com/TaWT9H3oZQ

— さのたけと (@taketo1024) 2017年11月28日

今回の記事に向けて、ホモロジー群を計算して可視化するツールを作りました。元々「数学とコンピュータ」 Advent Calendar を作ったときはこれを解説するつもりでいたのですが、ホモロジー群の説明に加えて実装の解説まで入れると詰め込みすぎなので、それはまたの機会とさせて下さい🙇

より高い視点から 〜 圏論の扉を開けてみる

第一回で「トポロジーでは同相写像で移り合う図形は同じと見なし、それによって変わらない性質を調べる」と書きました。ユークリッド幾何学の合同変換・相似変換に対して同相写像はあまりに自由度が高く、その下で図形を調べるのは手のつけようがなさそうでした。

そこで図形のホモロジー群という代数的にカチッと構造の決まる対象へと移したのでした。ホモロジーという手段を使って、幾何的な対象を代数的な対象に変換した訳です。このことを圏論の言葉では、

ホモロジー関手は、位相空間の圏からベクトル空間の圏への関手である。

と言います。「圏と関手」が強いのは、単に対象を別の対象へ移すだけでなく、対象間の関係性も一緒に移してしまうところです。つまり位相空間の間の連続写像（同相写像）をベクトル空間の間の線形写像（線形同型写像）に移してしまうのです。

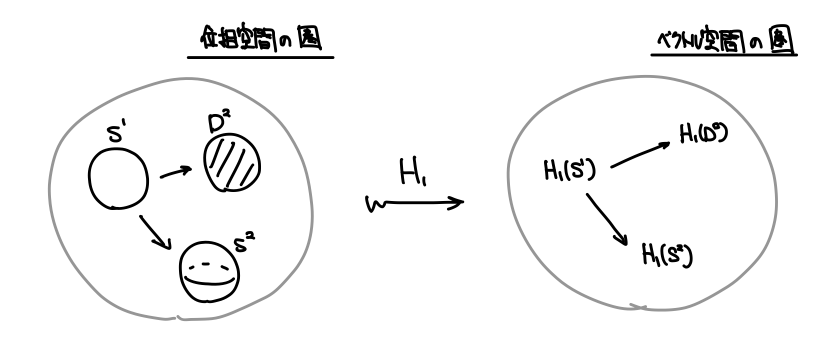
位相空間の圏で「同じ」ものが、ベクトル空間の圏でも「同じ」ものに移ってくれる。二つの図形が同相かどうかの判別は難しいですが、ホモロジー群がベクトル空間としての同型かはずっと簡単です。

このように現代数学では、関手を使って圏を丸ごと扱いやすい圏に移すことをよくします。このとき移った先で得られる情報が、元の圏の情報をどれだけ復元できるかというのは重要な問題です。閉曲面に関しては、ホモロジー関手は元の対象を完全に復元できる「十分いい」関手だった訳です。次元が上がると状況は絶望的に複雑になります⁵。

最後に

3回に渡って「トポロジーとは？」から「ホモロジー群の構成」まで書きました。トポロジーという言葉を初めて聞いた方や、数学専攻を志している人にとって興味を持つきっかけになれば幸いです。

まだホモロジー完全系列やホモロジーとコホモロジーのポアンカレ双対性など面白い話はたくさんあるので、追って記事を書きたいと思います。

ひとまずここまで読んで頂きありがとうございます。
メリークリスマス＆よいお年を🎉

参考図書

数学専攻でない人がトポロジーに入門するにはこちらがオススメです。特別な前提知識なく読めると思います（恐らく高校生でも）。

トポロジー:柔らかい幾何学

こちらはもう少し進んだ内容で、行列を使った具体的な計算やホモロジー群の位相不変性なども扱っています。

臨時別冊・数理科学2005年9月トポロジー入門

こちらは古典的なトポロジー（単体的複体のホモロジー群・基本群）の入門書です。

トポロジー【岩波全書】 (岩波オンデマンドブックス)

---

1. “In these days the angel of topology and the devil of abstract algebra fight for the soul of each individual mathematical domain.” Weyl, Hermann (1939), “Invariants”, Duke Mathematical Journal↩

2. 補足↩

3. 多くのトポロジーの入門書では整数係数でチェイン複体を構成します。その場合チェイン群はベクトル空間ではなく加群となります（係数環が体であるような加群を特にベクトル空間という）。しかし構成方法は変わらないので、この記事では R （または Q）係数を考えチェイン群はベクトル空間であるとします。↩

4. 補足↩

5. ポアンカレははじめ、1次元・2次元で言えるのと同様に3次元についても「ホモロジー群が3次元球面 S³ と同型になる閉多様体は、S³ と同相だろう」と予想しました。その後自ら反例となる「ポアンカレのホモロジー球面」を構成します。こうして次に「ホモトピー群が S³ と同型である閉多様体は、S³ と同相だろうか？」という問いを立てました。これが「ポアンカレ予想」で、提唱された 1904 年から約 100 年のときを経て 2002 年にロシア人の数学者 G・ペレルマン によって肯定的に解決されました。↩

トポロジーへの招待 〜 2. 切り貼りで作る色々な曲面

この記事は 数学とコンピュータⅡ Advent Calendar 18日目の記事です。

こんにちは、佐野です。前回の記事をたくさんの方に読んで頂けたようで嬉しいです。元々は 3 回で書き切るつもりでいたのですが、詰め込み過ぎてもよくないしちゃんと書きたい話はもっとあるので Advent Calendar 期間が過ぎてもシリーズを続けることにしました👍

1. 座標も補助線も使わない「やわらかい幾何学」
2. 切り貼りで作る色々な曲面 ←
3. ...

前回の復習

トポロジーは同相写像で移り合う図形を「同じ」と見なし、その同一視の下で変わらない図形の性質（位相不変量）を調べる分野でした。位相不変量の例として、多面体の頂点・辺・面の個数から決まるオイラー数を紹介しました。

今回は球面やトーラスなどの身近な曲面から、日常では決して見ることのない不思議な曲面まで色々と観察し、それらを区別するにはどうすればいいか考えていきましょう。

曲面いろいろ

0) 円板 D²

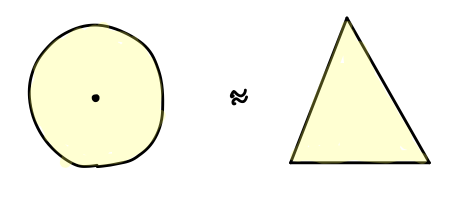
曲面と呼ぶにはつまらない例ですが、数学ではまず自明な例から始めことになっているので紹介します。円板 (disk)¹ は三角形（内部も含む）と同相であり、円周 S¹ がその境界です（肩に乗っている数がその図形の次元を現しています）。オイラー数は三角形の辺・頂点・面の数を数えて V - E + F = 1 です。

1) 球面 S²

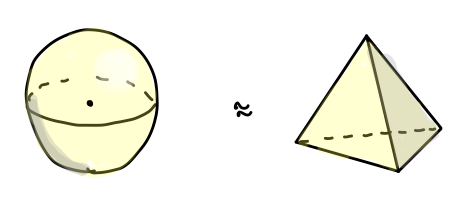
球面 (sphere) はトポロジーにおける最も基本的な閉曲面²です。前回、正多面体が球面と同相であることを述べましたが、トポロジカルには「穴の空いていない多面体」は全て球面です。そのオイラー数は等しく 2 となるのでした。

この先出てくる曲面の説明のためにも、多面体を使わずに紙を切り貼りして曲面を作る方法を紹介しましょう。下の長方形は自由に伸縮できる理想的な素材でできていると考えて下さい。がま口財布を閉じるように長方形の辺 a と a'、b と b' を張り合わせると球面ができます。

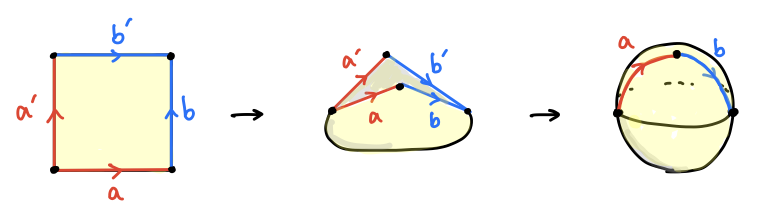
貼り合わせて作った図形は、頂点の数は 4 個のうち 2 個がくっついたので V = 3、辺は 4 個のうち 2 つずつペアになったので E = 2、面は一つだけなので F = 1 となり、この場合も V - E - F = 2 です。

別の作り方もあります。風呂敷で包むようにして長方形の周を一点に潰してしまいます³。

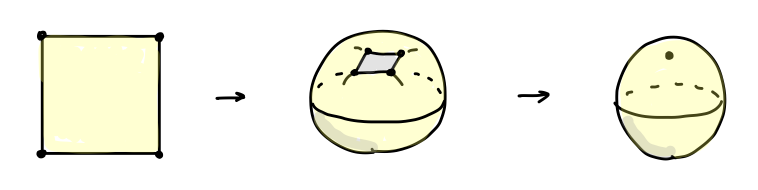
この場合、頂点は一つになるので V = 1、辺はなくなってしまったので E = 0、面は F = 1 なのでやはり V - E + F = 2 です。図画工作みたいで楽しいでしょ😙

2) トーラス T²

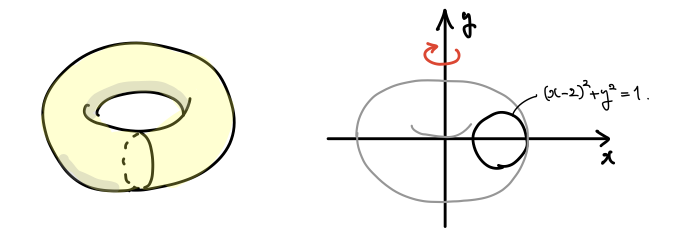
トーラスはドーナッツの表面に現れる閉曲面です。トポロジーでは球面の次に基本的な図形として出てきます。ユークリッド空間では、xy 平面上に y 軸から離れたところに円周をおいて y 軸に関して回転させることで得られます。

前回、多面体でトーラスを作って オイラー数 = 0 であることを見ました。これも長方形の切り貼りで作ることができます。今回は長方形で向かい合う辺の組み（a, a'）, (b, b') を貼り合わせます。

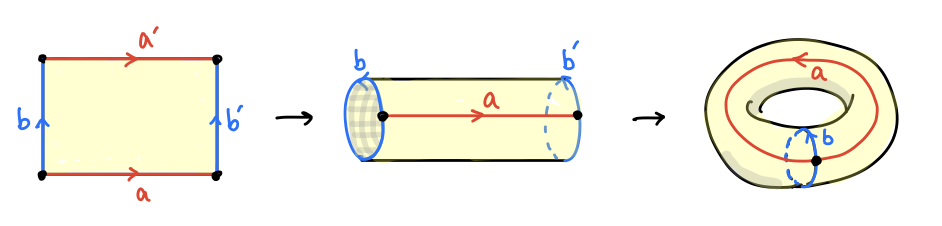
頂点は全て同一視されるので V = 1、あとは E = 2, F = 1 なので、やはり V - E + F = 0 です。

余談ですがファミコン／スーファミ世代にとってトーラスはお馴染みの空間です。RPG の世界では、マップ上で右端を過ぎると左端から出て、上端を過ぎると下端に出るので、境界で向かい合う辺が貼り合っていることになります。これは紛れもなくトーラスです。RPG の世界の「地球」は、トポロジカルにはドーナッツ形をしていることが分かります⁴。

3) ダブルトーラス T²#T²

ダブルトーラスはその名の通りトーラスを二個繋げた閉曲面です。これも前回、穴が二つ空いた多面体からオイラー数が -2 であることを見ました。実はこれも一枚の紙の貼り合わせで作れます。八角形の周上で、辺を一つおきにペアにして貼り合わせるできます。

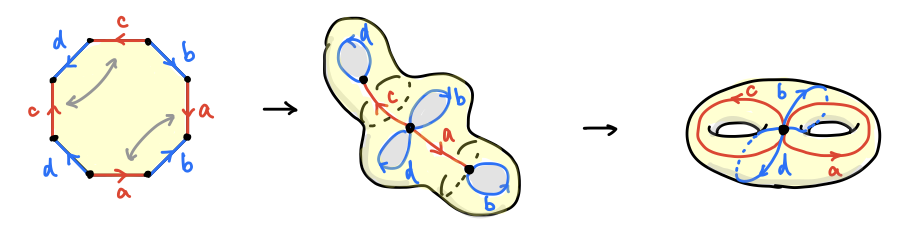
この作り方ビックリですよね。僕は図だけだと信じきれなかったので、粘土で作ってみたことがあります。

勤労感謝の日ってことで、八角形から種数2の閉曲面作るのやってみた。 pic.twitter.com/ghfRiZyZso

— さのたけと (@taketo1024) 2016年11月23日

さらにこのやり方で、好きな数だけ穴を空けた閉曲面が作れます。穴の数 g に対して、4g 角形の辺を一つおきに貼り合わせればいいのです。g = 3 の場合がこれです：

種数3にチャレンジ💪 pic.twitter.com/rfilvVVj6d

— さのたけと (@taketo1024) 2016年11月23日

穴が g 個空いた閉曲面のオイラー数は、頂点が一つで V = 1、辺は 4g 個あるものがペアになるので半分の E = 2g、面は F = 1 なので、オイラー数 2 - 2g となります。前回出した式が得られました！

こちらの CG動画 では 40角形 を貼り合わせて穴が 10 個あいた閉曲面を作っています（これを粘土でやるのはキツそう）。

4) メビウスの帯

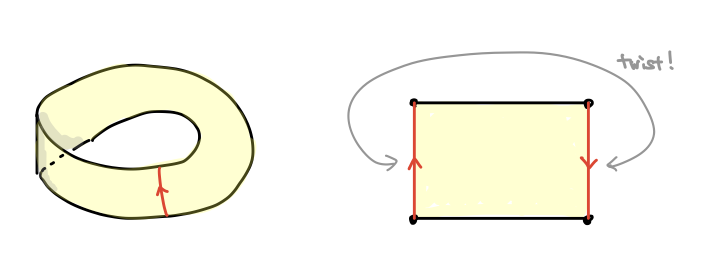
メビウスの帯を作ったことはありますか？なければ今、紙を帯状に切ってその両端を捻ってセロテープで貼り合わせて作ってみましょう。この図形は、中心線に沿ってグルッと一周するとスタート地点の裏側に着いてしまう 向き付け不可能⁵ な曲面です。

境界はどうなっているでしょう？指で帯のヘリをなぞってみると分かるように、一個の円周が二周巻きになったものが出てきます。オイラー数は 2 - 3 + 1 = 0 です。

ここからだんだん不思議なトポロジーの世界へ入って行きます👣

5) 射影平面 P²

長方形の向かい合う辺をトーラスの場合とは逆向きに貼り合わせてできる曲面が射影平面 (projective plane) です。これを実際に作ってみようとするとどうしても面がぶつかってできません。これは私たちが 3 次元空間で生きているからで、4 次元方向へ少しズラせば(!?) 面の交叉は回避できます。メビウスの帯を貼り合わせるのに平面から浮かせて 3 次元空間で行ったことと同じです。

右の図（交叉帽という）を見るときは、4 次元空間内の図形を 2 次元分落とした平面への影を見ていると考えましょう。交わっている部分はたまたま影が重なってそう見えているだけです。ただし交叉帽は射影平面を無理やりユークリッド空間に入れたときの姿なので、むしろ左の二つの展開図で理解した方が良いと思います。

もし RPG のマップが射影平面だったら、マップを一周して戻ってくるといつのまにか体が逆向きになってしまうでしょう。射影平面では全ての方向でメビウスの帯のような「裏返り」が起きます。なぜこんな訳の分からない図形を考えるのでしょう。

射影平面は球面の対蹠点を同一視した空間と見ることができます。この空間は、球面の中心を通る直線のパラメータ空間になっています。球面の前に平面を置いてこれをスクリーンと考えると、射影平面はこのスクリーンと、スクリーンとは交わらない「無限遠直線上の点たち」からなっています。

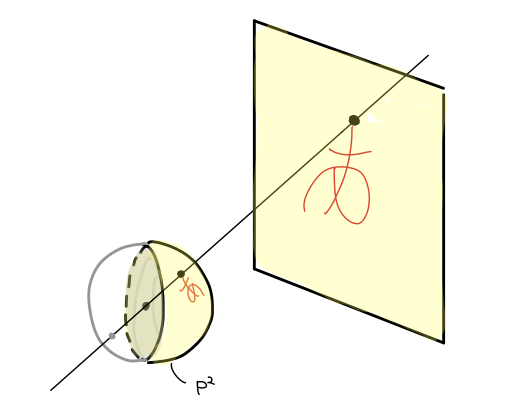
ユークリッド平面上の図形をこのスクリーンに映った影だと見ると、スクリーンを置く位置を変えることで平面上で交わる 2 直線の交点を「無限遠に飛ばして」平行にしてしまったり、放物線の「無限遠の交点」を手前に持ってきて楕円に変えることができたりします。ユークリッド平面上では魔法のように見える操作が射影平面では当たり前にできて、ユークリッド幾何学の範疇では複雑な定理も射影幾何学⁶では鮮やかに証明できてしまったりするのです。

射影平面のオイラー数は 2 - 2 + 1 = 1 です。

6) クラインの壷

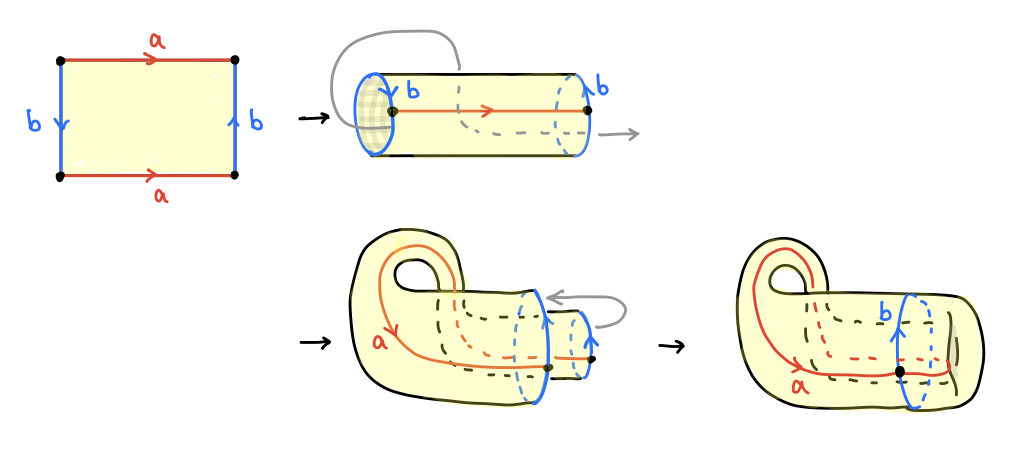
長方形の向かい合う辺の組のうち、一つは同じ向きに、もう一つは逆向きに貼り合わせた曲面がクラインの壷 (Klein bottle)です。これも向き付け不可能な曲面で、 3 次元空間の中で作ろうとすると面がぶつかってしまいますが、4 次元空間の中で面が交わらないように辺を貼り合わせることで壷のような形の図形が得られます。

これも向き付け不可能で、オイラー数は 1 - 2 + 1 = 0 です。

一旦まとめ

これらの曲面とその性質をまとめます：

これらの図形はどれも互いに同相ではありません。オイラー数だけを見ると重複しているものがありますが、三つの項目の組み合わせは一意です。実はこれは一般に言えることで、コンパクトな曲面は全てこの三つで分類できます。特に閉曲面（コンパクトで境界のない曲面）については、オイラー数と向きづけ可能性だけで分類できます。これが「閉曲面の分類定理」です。

とはいえ向きづけ可能性はオイラー数と比べて抽象的で捉えどころがない感じがします。何か複雑な多面体が与えられたとき、それが向きづけ可能かどうかは判定できるのでしょうか？

前回から残している疑問もあります：

• オイラー数 V - E + F は一体どこから出て来たのか？
• なぜこの量は位相不変となるのか？

この先これらの疑問への答えを得ることを目指し、図形の構造を取り出す具体的な方法を探って行きましょう。

今度は曲面をハサミで切ってみよう

まずは球面とトーラスをどう区別するかから考えてみましょう。
次は「ジョルダンの閉曲線定理」です：

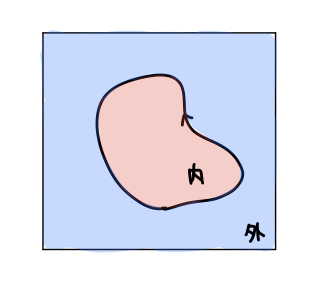
平面内の単純閉曲線は、平面を内側と外側の二つの領域に分ける。

あまりに当たり前のようで「こんなものが定理になるのか？」とすら感じられます。しかしその証明は難しく⁷、20世紀初頭にようやく得られました。何せ閉曲線の形が全く具体的に与えられていないのですから（至るところ滑らかでない病的な曲線かも知れません）。

いま注目したいのは、この「当たり前」は球面についてはそのまま成り立つが、トーラスについては成り立たないということです！球面はどんな風に切っても二つの部分に分かれてしまうが、トーラスにはそうならない切り方があります。

（他の曲面に対しても連結性を保つような切り方が色々とあります。展開図を見ながら試してみてください、特にメビウスの帯は楽しい！）

これは曲面の繋がり方（位相 = トポロジー）を区別する性質と言えそうです。 それでは二つに分かれる切り方と分かれない（連結性を保つ）切り方の違いはなんでしょう？

二つに分かれる切り取り線は、曲面の一部分であった二つの曲面の境界となっています。曲面の一部分の境界として現れるようなキリトリ線に沿って切れば、曲面は二つに分かれる訳です。逆に曲面の一部分の境界でないようなキリトリ線に沿って切れば、連結性は保たれることになります。

連結性を保つような切り方はどれぐらいあるのでしょうか？この情報を持っているのが図形の 1次ホモロジー群 です。 次回、曲面のホモロジー群を定義し、閉曲面がホモロジー群によって完全に分類されることを見ていきましょう！

参考図書

前回紹介した二つの本には「閉曲面の分類定理」が載っています。多角形から閉曲面を作る議論を一般に行い、曲面を何度も切ったり貼ったりすることで標準形に変形するという議論をします。

トポロジー:柔らかい幾何学

トポロジー【岩波全書】 (岩波オンデマンドブックス)

面白いトポロジーの絵をもっと見たいという方にはコチラがオススメです。中世の解剖学書か？と思えるような楽しい（グロテスクな）絵がたくさん出てきます。

トポロジーの絵本 新装版 (シュプリンガー数学リーディングス)

少し触れた射影幾何学の入門書はこちらがオススメです。

射影幾何学の考え方 (数学のかんどころ 19)

---

1. 単に「円」というと内部を含むのか含まないのかハッキリしないので、内部を含む場合は 円板 (disk) といい、含まない場合は 円周 (circle) と言います。↩

2. コンパクトで境界のない曲面を 閉曲面 と言います。この 閉 は閉集合の 閉 とは別です。例えば円板は閉曲面ではありませんが（円周がその境界なので）ユークリッド空間の中では閉集合です。↩

3. 「こんな貼り合わせ方アリなの？」と思われたかも知れません。この作り方で得られる図形は多面体ではなく、より一般に 胞体 と呼ばれるものです。胞体についても多面体と同じやり方でオイラー数が求められるのは、それぞれのホモロジー群が同型であるという事実に依っています。↩

4. FF4 で月から地球(?)に戻って来るときに球体のようなものが見えた気がするのですが、球面とトーラスは同相でないのでちょっと不思議です。↩

5. 向き (orientation) は 方向 (direction) とは別の概念です。3次元空間内の曲面の向きとは、その法線（曲面に直行する直線）の方向のことで、つまりは曲面の表裏のことです。より一般の状況での向きの定義はもっと難しくなります。↩

6. このような変換を射影変換といい、射影変換で不変な不変量を調べるのが射影幾何学です。↩

7. まさしくその証明にホモロジー理論を使います。従ってホモロジー理論の導入にジョルダンの閉曲線定理を使うのは循環論法になりますが、ここでは日常的な「当たり前」の感覚に頼って話を進めることにします。↩

トポロジーへの招待 〜 1. 座標も補助線も使わない「やわらかい幾何学」

この記事は 数学とコンピュータⅡ Advent Calendar 11日目の記事です。

こんにちは、佐野です。12月といえば Advent Calendar の季節です🎄思いつきで 数学とコンピュータ Advent Calendar Ⅰ / Ⅱ を立ち上げたところ、嬉しいことに二つともすぐに満員となりました。エントリーして下さった皆さん、ありがとうございます🙇

僕は全3回でトポロジーの考え方と計算手法を、自作のプログラムを使いながら説明していこうと思います。

1. 座標も補助線も使わない「やわらかい幾何学」 ← イマココ
2. 切り貼りで作る色々な曲面
3. ...

このシリーズを通して トポロジーは最高に自由で楽しい数学（の一つ）である ことをお伝えできたら幸いです！

「やわらかい幾何学」って何？

「コーヒーカップを、取っ手の輪っかを残すように変形するとドーナッツの形にできる。従ってコーヒーカップとドーナッツは同じ。」と主張するのがトポロジーです。

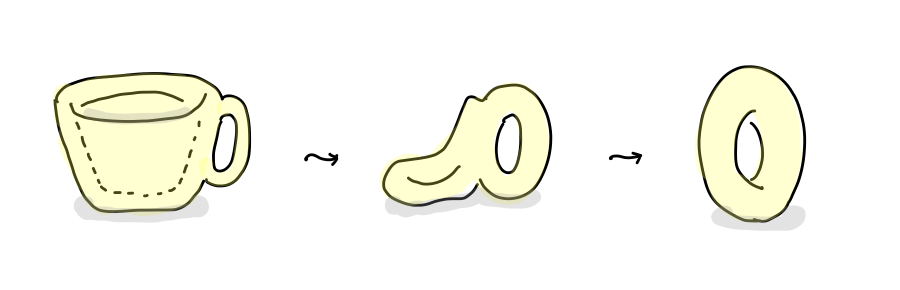
小学校や中学校で習うユークリッド幾何学では、三角形や四角形などの図形はカチッと固まっており、長さや角度を計ることはあってもグニャグニャと形を変えるようなことはしませんでした。この「硬さ」と対比して、どんな連続的な変形も受け入れるトポロジーは「やわらかい幾何学」だと言われます。

数学といえば厳密だというイメージがあると思います。しかし「コーヒーカップとドーナッツは同じ」などという主張はいかにもいい加減で、数学の土俵に乗ることすら許されないように思われます。その感覚は真っ当で、だからこそユークリッド幾何学からトポロジーの誕生まで 2,000 年以上ものときを要したのだとも言えます。トポロジーでは円や多角形などの「綺麗な図形」だけでなく、歪んだ紐や穴の空いた曲面などの「日常で目にする図形¹」も数学として扱うのです。

もし数学が「綺麗な図形」しか扱わない（扱えない）お堅い学問だというイメージをお持ちなら、トポロジーの自由さ（とそれに伴う絶望的な難しさ）を前にその中世的な数学観を喜んで破砕して下さい👊

そもそも「幾何学」とは何か？

19世紀末にトポロジーを創設したアンリ・ポアンカレは 「数学とは、異なるものを同じものと見なす技術である」²と言ったそうです。…とだけ言われて「コーヒーカップとドーナッツは同じだ」と受け入れるのは難しいと思うので、少し立ち返って、私たちはどのように図形を「同じ」と見なしているのか観察してみましょう。

ユークリッド幾何学では次の二つの三角形は「同じ」であると考えます。しかし改めて考えると三角形が置かれてる位置や傾きは異なっています。どうしてこれが「同じ」だと言えるのでしょう？（難しい言葉を使わず4歳児に説明するとしたらどう言いますか？）

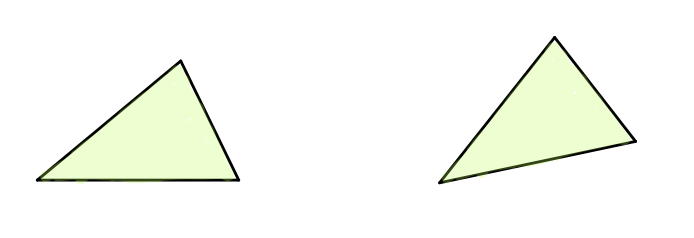
それは、左の三角形を持ち上げて動かせば右の三角形にピタッと重ねることができるからです。このとき二つの三角形は「合同」というのでした。

ユークリッド幾何学にはもう一つ「相似」という関係もあります。これは「合同」よりも広い「同じ」です。長さや面積のような「絶対的な量」でなく、長さの比や角度などの「相対的な量」を扱うときに便利な関係です。

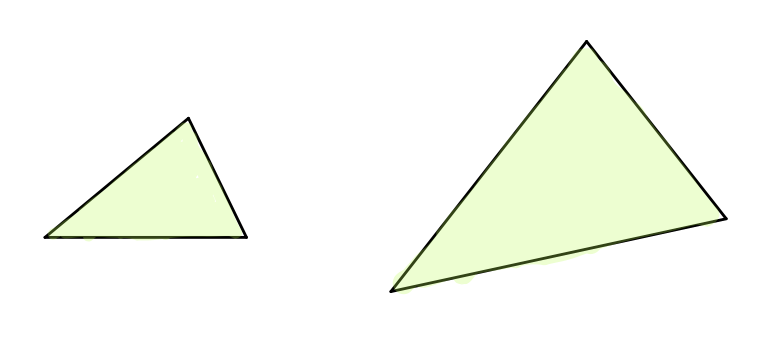
上の二つの三角形が「相似」であると言えるのは、左の三角形を縦横均等に拡大して移動することで右の三角形にピタッと重ねることができるからです。この拡大縮小が「縦横均等」であることが大切で、横方向にだけビヨーンと伸ばす³ような変形は許されていません。

この二つの例を見るだけでも、私たちは中学校までに二通りの「図形を同じと見なす技術」を学んでいることが分かります。その技術とは「特定の操作で図形を動かして一方を他方にピタッと重ねること」です。

ここで19世紀の数学者クラインによる「幾何学とは何か？⁴」に対する答えを見てみましょう：

幾何学的性質とは、それに作用する 変換群の作用で不変に保たれる性質 のことである。

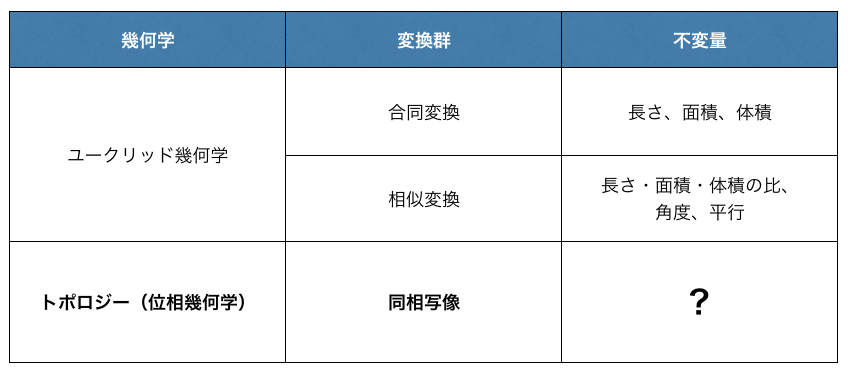
「変換群」という難しい言葉が出てきましたが、合同の例では「合同変換（回転・平行移動・鏡映）の全体」、相似の例では「相似変換（合同変換＋拡大縮小）の全体」のことです。合同変換で不変に保たれるのは「長さ・面積・体積・角度」などで、相似変換で保たれるのは「長さや面積の比・角度」などです。クラインの立場では、

「ユークリッド幾何学は、合同変換や相似変換によって不変に保たれる性質を調べる学問である」

ということになります。

ではトポロジーは？

「トポロジーとは何か？」に答えるには、トポロジーにおける「同じと見なすための変換」が何かを答えれば良いことになります。それがコーヒーカップをドーナッツに変えるときに行った「連続的な変形^{5 6}」です。ここで図形を一点に潰してしまうような変形まで認めると「全ての図形は一点と同じ」という役立たずな理論が出来上がってしまうので「可逆 = 元に戻せる」ものに限ることにします。

「可逆で、行きも戻りも連続であるような変換」

このような変換（写像）を同相写像と言い、同相写像によって移り合う二つの図形は同相（位相同型）であると言います。すると、

「トポロジーは、同相な図形同士で不変に保たれる性質（位相不変量）を調べる学問である」⁷

と述べることができるようになりました。つまり「コーヒーカップとドーナッツにおいて共通しているものは何か？」を問うのがトポロジーということです！

ところで「同相な図形は同じ」と見なしたいケースとはなんでしょう？その答えはトポロジーの起源とも言われる「ケーニスベルクの問題」で見ることができます。

「この7つの橋を全て、同じ橋を2度通ることなく渡り、元の所に帰ってくることができるか」という問題です。18世紀の数学者オイラーは、川で囲われた領域を点、橋で繋がっている点同士を辺とするグラフを対応させることで、それは不可能であると証明しました。

問題は「このグラフは一筆書きできるか」となり、その本質はグラフの構造、つまりどの点と点がどの繋がっているかです。実際の町における移動距離や、絵に描いたグラフの辺の長さなどは関係ありません。このケースでは「同相なグラフは同じと見なす」のが正しいアプローチだと分かります。

同相写像で保たれる性質とは？

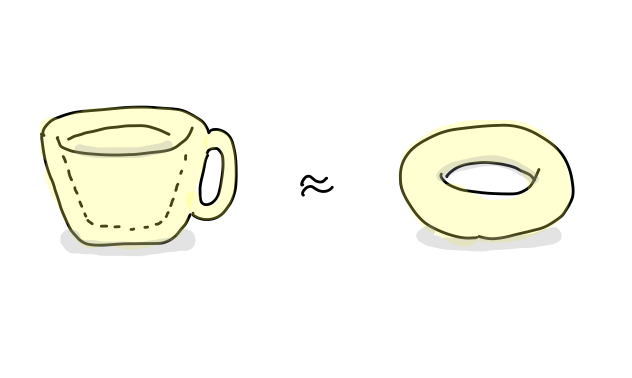
さて、二つの図形を眺めながら、何が共通していると言えるか考えてみましょう。もしこれらが粘土でできており、一方を他方に変形したのなら二つの「体積」は等しいでしょう。しかし一般に同相写像は相似変換も含んでおり、相似変換は自由に大きさを変えてしまうので「体積」は位相不変とは言えません。長さや角度を計ろうとするのも無意味です。もっと素朴に（幼児のように）考えてみましょう。

(1) 連結性

コーヒーカップもドーナッツも「一個のもの」です。コーヒーカップの取っ手の部分を切り離してしまえば図形は二つの部分に分かれます。「切り離す」というのは図形の繋がりを壊す操作ですから連続ではありません。コーヒーカップをドーナッツに変形する過程では「図形が二つ以上のものに分かれる」ことはないので「繋がった状態 = 連結性⁸」は保たれています。これは一つの位相不変な性質です。

(2) コンパクト性

二つの図形は有限な大きさを持つ閉じた図形です（宇宙のように無限に広がっていません）。このような図形はコンパクトであると言い、コンパクトな図形が連続写像によって無限に広がってしまうことはないので⁹、これも位相不変な性質です。

(3) 穴の数

ドーナッツには穴があります¹⁰。コーヒーカップも、取っ手の部分が輪っかになっているので¹¹穴が空いています。図形を連続的に変形する過程では新たに穴が空いてしまったり埋まってしまったりすることはないので、同相写像によっては「穴の数」は保たれます。「穴の数」は上の二つと違って、数として得られる位相不変量です。

これらの性質や量は対象の図形が簡単であれば見てすぐに分かりますが、もっと複雑な図形の場合はそうは行きません。例えば 4 次元の図形が与えられて、穴が何個空いてるかを見て調べるのは一般人には不可能でしょう。何かしらもっと体系的に位相不変量を取り出す方法が欲しくなります。その本格的な手段は次回説明することにし、今回は導入として、トポロジーが創設される以前から知られていた位相不変量であるオイラー数を紹介します。

オイラー数

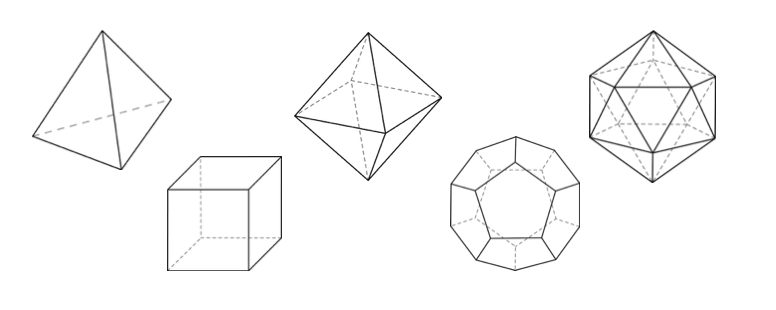
5つの正多面体があります。下の表にぞれぞれの頂点 (V: Vertex)・辺 (E: Edge)・面 (F: Face) の数が書かれています。多面体ごとにこれらの数は異なります。しかし、これらの数の組に対してある計算をすると、不思議と共通の値が出てきます。

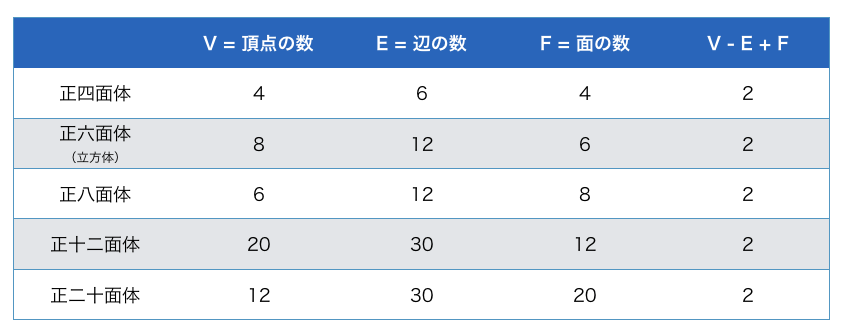
V - E + F を計算すると、全て 2 です。

どんな多面体についても V - E + F = 2 となるのでしょうか？ 答えは NO です。次の図形について計算してみると、

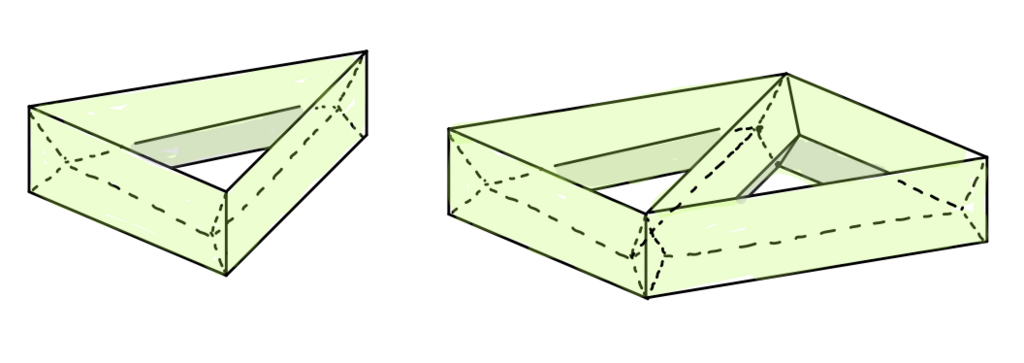
左は V - E + F = 0、右は V - E + F = -2 です。

パターン見えて来ましたね…！どうやら球面に同相な多面体は V - E + F = 2 となり（内側をプクッと膨らませるとどれも球面になりますよね）、穴の数が増えるごとに値が 2 ずつ減っていくようです。つまり穴の数を として、

となっているようです。

この量が (多面体の) オイラー数です。こんな単純な式で計算される量が位相不変であるというのは実に不思議です。例えば球面を 4 個の頂点で分割しても 5000兆個 の頂点で分割しても、オイラー数は等しく 2 となるのです。「同相であれば値が等しい」のが位相不変量なので、対偶を取れば「位相不変量が異なれば同相でない」となります。球面とトーラス（ドーナッツの表面）が同相でないという事実は、2 ≠ 0 から直ちに分かってしまう訳です。

では逆に「オイラー数が等しい図形は同相だ」と言えるでしょうか？ 答えは NO です。例えばこの変な図形：

オイラー数は 0 です（数えて見てください）。どう見ても上に出てきたもの同相ではありません。 以上をまとめると、

• オイラー数は図形に対して組み合わせ的に定まる量であり、
• 同相な図形に対してはオイラー数は一致するが、
• オイラー数が一致するからといって同相とは限らない。

となります。ここで当然の疑問として、

• V - E + F という数は一体どこから出て来たのか？
• なぜこの量は位相不変となるのか？

が残ると思います。 次回、単体複体のホモロジー群 を導入し、この数の由来を探って行くことにしましょう。

完全な不変量を求めて

「オイラー数が等しくても同相とは限らない」は、ユークリッド幾何学において「合同な三角形の面積は等しい」は成り立つが「面積の等しい三角形は合同」とは限らないという事情と同じです。

しかし「三角形の合同条件」には「三辺相等」「ニ辺夾角相等」「ニ角夾辺相等」がありました。これは三角形の「辺の長さ」や「角度」などの不変量をうまく組み合わせることで 逆 が言えてしまうという強い定理です。

二つの図形の間で変換が作れるかどうかという問題は、いわば無限次元空間の中で「点」を探すことであり、一般にはとても難しいものです。一方で具体的に計算できる不変量を組み合わせることで「同型でない」だけでなく「同型である」までも判定できるとしたら、それは対象の図形がその不変量によって完全に決定されるということです。

オイラー数は位相不変量としては完全ではありませんでした。しかし対象とする図形を制限し、他の不変量と組み合わせることで、特定の図形が完全に分類できるということも次回説明します。お楽しみに！

参考図書

数学専攻でない人がトポロジーに入門するにはこちらがオススメです。特別な前提知識なく読めると思います（恐らく高校生でも）。

トポロジー:柔らかい幾何学

こちらはもう少し進んだ内容で、行列を使った具体的な計算やホモロジー群の位相不変性なども扱っています。

臨時別冊・数理科学2005年9月トポロジー入門

こちらは古典的なトポロジー（単体的複体のホモロジー群・基本群）の入門書です。

トポロジー【岩波全書】 (岩波オンデマンドブックス)

さらに進んで学びたい人は、オンラインで入手できる A.Hatcher の "Algebraic Topology" を見てみると良いと思います。

---

1. もちろんトポロジーでは「日常で目にする図形」だけでなく「人間には見ることのできない図形」も扱います。↩

2. “la mathématique est l'art de donner le même nom à des choses différentes.” Science et Méthode, 1908. ↩

3. そのような変形は「アフィン変換（線形変換＋平行移動）」と呼ばれ、アフィン変換で移り合う図形を同一視する幾何学が「アフィン幾何学」です。↩

4. このような「問い」が19世紀になってようやく起きた背景には、ギリシャ時代以来「ユークリッド幾何学」が唯一絶対の幾何学だと信じられてきたのに対し、18世紀以降その公理を満たさない「非ユークリッド幾何学」も成り立つことが明らかになってきたことがあります。↩

5. ユークリッド空間における「写像の連続性」を定めるのが 論法です（過去記事）。トポロジーにおいてはより一般の「位相空間（topological space）」を扱いますが、「位相」「連続写像」の厳密な定義は大幅に直観を離れてしまうので、wikipedia へのリンクだけ貼ってここでは述べないことにします。↩

6. 正確には二つの図形が「同相」であることと「アイソトピック」であること（ある空間の中で同相を保ちながら一方を他方に変形できること）は異なります。「コーヒーカップとドーナッツ」の例では の中でアイソトピーを作っており、その結果として二つの図形は同相となっています。↩

7. トポロジーでは「同相」よりも遥かに広い「ホモトピー同値」という同値関係も扱います。例えば と 1点、円周とメビウスの帯などは互いにホモトピー同値になります。↩

8. 「連結」「コンパクト」にもちゃんと厳密な定義があります。↩

9. 「有界 = 有限の大きさを持っている」だけではダメです。例えば 内の半径 1 の円板で境界の円周を除いたもの（開円板）は と同相になります。あるいは長さ 1 の開区間 は実数直線 と同相です。面積や長さは等しくても、境界を含んでいるか否か（図形が閉じているか否か）で位相的な性質は決定的に変わってしまいます。↩

10. Oxford Dictionary における doughnut の定義 には “Typically in the shape of a ball or ring.” とあるので、「穴が空いてる」ことがその定義に含まれる訳ではないようです。↩

11. 取っ手の部分が輪っかになっていない 例外的なカップ もあるようです。↩